题目内容
(1)如图,点A、B、C、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.
(2)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,tanC=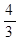 ,求腰AB的长.
,求腰AB的长.

(2)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,tanC=
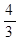 ,求腰AB的长.
,求腰AB的长.
(1)证明见解析;(2)4.
试题分析:(1)根据BE∥DF,可得∠ABE=∠D,再利用ASA求证△ABC和△FDC全等即可;
(2)过D作DE⊥BC于E,因为AD∥BC,AB,DE都和BC垂直,那么四边形ADEB就是个矩形.AD=BE,EC=BC-AD,在直角三角形CDE中,有了CE的值,又知道tanC的值,求出DE就不难了.
试题解析:(1)证明:∵BE∥DF,
∴∠ABE=∠D,
在△ABE和△FDC中,
∵
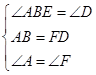 ,
,∴△ABE≌△FDC(ASA),
∴AE=FC;
(2)解:如图2,作DE⊥BC于E,
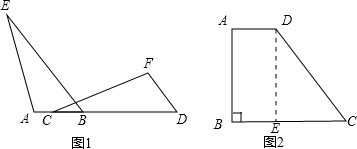
∵AD∥BC,∠B=90°,
∴∠A=90°.又∠DEB=90°,
∴四边形ABED是矩形.
∴BE=AD=2,∴EC=BC-BE=3.
在Rt△DEC中,DE=EC•tanC=3×
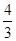 =4.
=4.
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形. ,AC=1+
,AC=1+ ,BC=2,⊙O的直径BE交AC于点D.
,BC=2,⊙O的直径BE交AC于点D.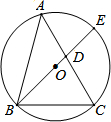

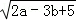 +(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
+(2a+3b﹣13)2=0,则此等腰三角形的周长为( )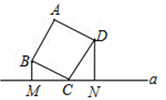

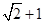 B.
B. C.
C. D.
D.
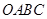 放在平面直角坐标系中,
放在平面直角坐标系中, 是原点,
是原点, 的坐标为(1,
的坐标为(1, ),则点
),则点 的坐标为( )
的坐标为( )