题目内容
如图,在平面直角坐标系中放置一直角三角板,其顶点为 ,
,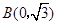 ,
,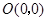 ,将此三角板绕原点
,将此三角板绕原点 顺时针旋转
顺时针旋转 ,得到
,得到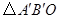 .
.
(1)如图,一抛物线经过点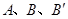 ,求该抛物线解析式;
,求该抛物线解析式;
(2)设点 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点
的面积达到最大时点 的坐标及面积的最大值.
的坐标及面积的最大值.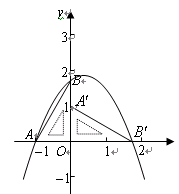
 ,
,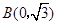 ,
,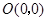 ,将此三角板绕原点
,将此三角板绕原点 顺时针旋转
顺时针旋转 ,得到
,得到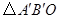 .
.(1)如图,一抛物线经过点
 ,求该抛物线解析式;
,求该抛物线解析式;(2)设点
 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点
的面积达到最大时点 的坐标及面积的最大值.
的坐标及面积的最大值.
解:(1)∵抛物线过
设抛物线的解析式为
又∵抛物线过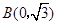 ,将坐标代入上解析式得:
,将坐标代入上解析式得:
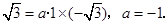

即满足条件的抛物线解析式为
(2)(解法一):如图1,∵ 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,

设 则
则
 点坐标满足
点坐标满足
连接

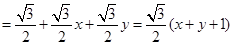
=
当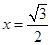 时,
时, 最大.
最大.
此时, .即当动点
.即当动点 的坐标为
的坐标为 时,
时,
 最大,最大面积为
最大,最大面积为
(解法二):如图2,连接
 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,

 且
且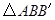 的面积为定值,
的面积为定值,
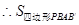 最大时
最大时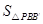 必须最大.
必须最大.
∵ 长度为定值,∴
长度为定值,∴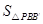 最大时点
最大时点 到
到 的距离最大.
的距离最大.
即将直线 向上平移到与抛物线有唯一交点时,
向上平移到与抛物线有唯一交点时,
 到
到 的距离最大.
的距离最大.
设与直线 平行的直线
平行的直线 的解析式为
的解析式为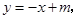
联立
得
令
解得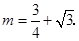 此时直线
此时直线 的解析式为:
的解析式为: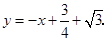
 解得
解得
∴直线 与抛物线唯一交点坐标为
与抛物线唯一交点坐标为
设 与
与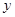 轴交于
轴交于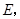 则
则
过 作
作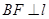 于
于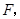 在
在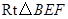 中,
中,
过 作
作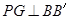 于
于 则
则 到
到 的距离
的距离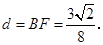
此时四边形 的面积最大.
的面积最大.
∴ 的最大值=
的最大值=
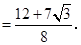

设抛物线的解析式为

又∵抛物线过
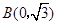 ,将坐标代入上解析式得:
,将坐标代入上解析式得: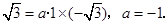

即满足条件的抛物线解析式为

(2)(解法一):如图1,∵
 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,
设
 则
则
 点坐标满足
点坐标满足
连接


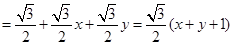
=

当
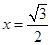 时,
时, 最大.
最大.此时,
 .即当动点
.即当动点 的坐标为
的坐标为 时,
时, 最大,最大面积为
最大,最大面积为
(解法二):如图2,连接

 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,
 且
且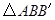 的面积为定值,
的面积为定值,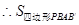 最大时
最大时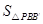 必须最大.
必须最大.∵
 长度为定值,∴
长度为定值,∴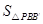 最大时点
最大时点 到
到 的距离最大.
的距离最大.即将直线
 向上平移到与抛物线有唯一交点时,
向上平移到与抛物线有唯一交点时, 到
到 的距离最大.
的距离最大.设与直线
 平行的直线
平行的直线 的解析式为
的解析式为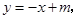
联立

得

令

解得
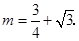 此时直线
此时直线 的解析式为:
的解析式为: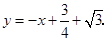
 解得
解得
∴直线
 与抛物线唯一交点坐标为
与抛物线唯一交点坐标为
设
 与
与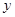 轴交于
轴交于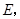 则
则
过
 作
作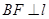 于
于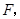 在
在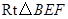 中,
中,
过
 作
作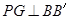 于
于 则
则 到
到 的距离
的距离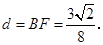
此时四边形
 的面积最大.
的面积最大.∴
 的最大值=
的最大值=
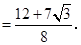
(1)由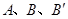 三点的坐标根据待定系数法即可求出解析式;
三点的坐标根据待定系数法即可求出解析式;
(2)先根据题意列出函数关系式,再根据函数关系式的特征即可得到最大值。
 三点的坐标根据待定系数法即可求出解析式;
三点的坐标根据待定系数法即可求出解析式;(2)先根据题意列出函数关系式,再根据函数关系式的特征即可得到最大值。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 交于A(-1,0)、B(3,0)两点,与
交于A(-1,0)、B(3,0)两点,与 轴交于点C(0,3),求抛物线的解析式;
轴交于点C(0,3),求抛物线的解析式;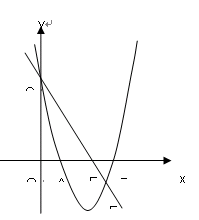
 ,A与
,A与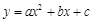 上,且这条抛物线与
上,且这条抛物线与 轴的交点的纵坐标为-6,求这条抛物线的顶点坐标.
轴的交点的纵坐标为-6,求这条抛物线的顶点坐标.
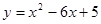 的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线
的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线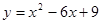 .
.
 与函数
与函数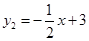 的图象大致如图.若
的图象大致如图.若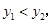 则自变量
则自变量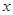 的取值范围是( ).
的取值范围是( ).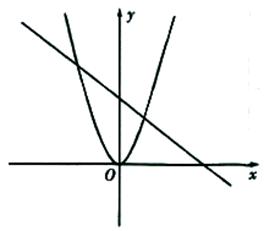
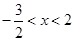

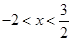

 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为 ,则点D的横坐标最大值为( )
,则点D的横坐标最大值为( )
 (x>0),若该车某次的刹车距离为5 m,则开始刹车时的速度为( )
(x>0),若该车某次的刹车距离为5 m,则开始刹车时的速度为( )