题目内容
如图,已知二次函数y=ax2+bx+c的图象经过A(1,0)、B(5,0)、C(0,5)三点。
(1)求这个二次函数的解析式;
(2)过点C的直线y=kx+b与这个二次函数的图象相交于点E(4,m),请求出△CBE的面积S的值。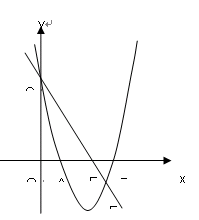
(1)求这个二次函数的解析式;
(2)过点C的直线y=kx+b与这个二次函数的图象相交于点E(4,m),请求出△CBE的面积S的值。

解:(1)∵二次函数y=ax2+bx+c的图象经过A(1,0)、B(5,0)、C(0,5)三点,
∴y=a(x-1)(x-5),把C(0,5)代入得:5=5a,解得:a=1,
∴y=(x-1)(x-5),y=x2-6x+5,
∴二次函数的解析式是y=x2-6x+5.
(2)∵y= x2-6x+5,∴当x=4时,m=16-24+5=-3,∴E(4,-3),
设直线EC的解析式是y=kx+b, 把E(4,-3),C(0,5)代入得: ,解得:k=-2, b=5,
,解得:k=-2, b=5,
∴直线EC的解析式是y=-2x+5,
当y=0时0=-2x+5,解得:x= ,∴M的坐标是(
,∴M的坐标是( ,0) ∴BF=5-
,0) ∴BF=5- =
= ,
,
∴S△CBE=S△CBF+S△BFE=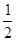 ×
× ×5+
×5+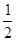 ×
× ×3="10" ,
×3="10" ,
答:△CBE的面积S的值是10.
∴y=a(x-1)(x-5),把C(0,5)代入得:5=5a,解得:a=1,
∴y=(x-1)(x-5),y=x2-6x+5,
∴二次函数的解析式是y=x2-6x+5.
(2)∵y= x2-6x+5,∴当x=4时,m=16-24+5=-3,∴E(4,-3),
设直线EC的解析式是y=kx+b, 把E(4,-3),C(0,5)代入得:
 ,解得:k=-2, b=5,
,解得:k=-2, b=5,∴直线EC的解析式是y=-2x+5,
当y=0时0=-2x+5,解得:x=
 ,∴M的坐标是(
,∴M的坐标是( ,0) ∴BF=5-
,0) ∴BF=5- =
= ,
,∴S△CBE=S△CBF+S△BFE=
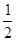 ×
× ×5+
×5+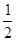 ×
× ×3="10" ,
×3="10" , 答:△CBE的面积S的值是10.
(1)根据二次函数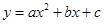 的图象经过A(1,0)、B(5,0)、C(0,5)三点,得到y=a(x-1)(x-5),把C的坐标代入就能求出a的值,即可得出二次函数的解析式;
的图象经过A(1,0)、B(5,0)、C(0,5)三点,得到y=a(x-1)(x-5),把C的坐标代入就能求出a的值,即可得出二次函数的解析式;
(2)把E的坐标代入抛物线即可求出m的值,设直线EC的解析式是y=kx+b,把E、C的坐标代入就能求出直线EC,求直线EC与X轴的交点坐标,过E作EN⊥X轴于N,根据点的坐标求出△CBM和△BME的面积,相加即可得到答案.
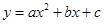 的图象经过A(1,0)、B(5,0)、C(0,5)三点,得到y=a(x-1)(x-5),把C的坐标代入就能求出a的值,即可得出二次函数的解析式;
的图象经过A(1,0)、B(5,0)、C(0,5)三点,得到y=a(x-1)(x-5),把C的坐标代入就能求出a的值,即可得出二次函数的解析式;(2)把E的坐标代入抛物线即可求出m的值,设直线EC的解析式是y=kx+b,把E、C的坐标代入就能求出直线EC,求直线EC与X轴的交点坐标,过E作EN⊥X轴于N,根据点的坐标求出△CBM和△BME的面积,相加即可得到答案.

练习册系列答案
相关题目

 每亩树苗的收益)
每亩树苗的收益) ,
, )
) 经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m,
经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m, ),点C是抛物线在第三象限的一点,且横坐标为-2.
),点C是抛物线在第三象限的一点,且横坐标为-2.
 ,
,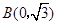 ,
,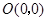 ,将此三角板绕原点
,将此三角板绕原点 顺时针旋转
顺时针旋转 ,得到
,得到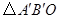 .
.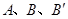 ,求该抛物线解析式;
,求该抛物线解析式; 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点
的面积达到最大时点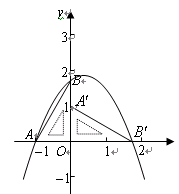

 的图象如图所示,则
的图象如图所示,则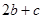 的值是( )
的值是( )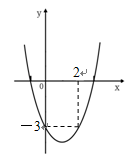
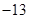
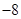
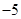
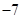
 ,下列说法正确的是( )
,下列说法正确的是( )

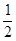 (x+1)2
(x+1)2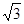 x2
x2 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是
的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是 ,则a+b+c=________.
,则a+b+c=________.