题目内容
如图所示,在3×3的正方形网格中每个小正方形的边长都是1,每个小格的交点叫做格点,以格点为顶点,分别按下列要求画三角形:(1)请网格图中作一个三边长分别 为3,
| 2 |
| 5 |
(2)画一个三角形均为无理数的等腰直角三角形(不要求证明),并求出其面积.
分析:根据正方形网格的边长为1,连接不在一条直线上的两个格点,得到直角三角形,利用勾股定理求得连线的长即可.
解答: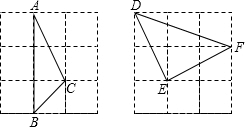 解:(1)如图:∵正方形网格中每个小正方形的边长都是1,
解:(1)如图:∵正方形网格中每个小正方形的边长都是1,
∴AB=3,AC=
=
,BC=
=
,
∴△ABC即为所求的三边长分别 为3,
,
的三角形.
(2)DE=
=
,EF=
=
DF=
=
∴S△DEF=
DE•EF=
×
×
=
 解:(1)如图:∵正方形网格中每个小正方形的边长都是1,
解:(1)如图:∵正方形网格中每个小正方形的边长都是1,∴AB=3,AC=
| 12+22 |
| 5 |
| 12+12 |
| 2 |
∴△ABC即为所求的三边长分别 为3,
| 2 |
| 5 |
(2)DE=
| 12+22 |
| 5 |
| 12+22 |
| 5 |
DF=
| 12+32 |
| 10 |
∴S△DEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
点评:本题考查了勾股定理的应用,近几年的中考中此类考题出现的频率大大增加.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 如图所示,在4×4的方格中每个小正方形的边长是单位1,小正方形的顶点称为格点.现有格点A、B,在方格中任意找一个格点C,则以A、B、C三点为顶点能构成等腰三角形的概率是
如图所示,在4×4的方格中每个小正方形的边长是单位1,小正方形的顶点称为格点.现有格点A、B,在方格中任意找一个格点C,则以A、B、C三点为顶点能构成等腰三角形的概率是 如图所示,在5×5的方格纸上建立直角坐标系,A(1,0),B(0,2),试以5×5的格点为顶点作△ABC与△OAB相似(相似比不为1),并写出C点的坐标.
如图所示,在5×5的方格纸上建立直角坐标系,A(1,0),B(0,2),试以5×5的格点为顶点作△ABC与△OAB相似(相似比不为1),并写出C点的坐标. 如图所示,在一圆柱体的下底边沿A处,不走直线而绕着圆柱侧面,沿一条螺旋形路线绕到B处的最短路线是什么?
如图所示,在一圆柱体的下底边沿A处,不走直线而绕着圆柱侧面,沿一条螺旋形路线绕到B处的最短路线是什么? 如图所示,在3×3的方格内,填写了一些式子和数,图中各行、各列及对角线上三个数之和都相等,请你求出x、y、z的值.
如图所示,在3×3的方格内,填写了一些式子和数,图中各行、各列及对角线上三个数之和都相等,请你求出x、y、z的值.