题目内容
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
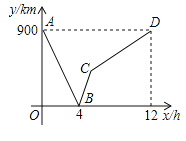
(1)甲、乙两地之间的距离为 千米;图中点B的实际意义是 ;
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
【答案】(1)900,4小时两车相遇.
(2)所以线段BC所表示的y与x之间的函数关系式为:y=225x﹣900(4≤x≤6)
(3)第二列快车比第一列快车晚出发0.75小时
【解析】
试题(1)根据观察图象,可得甲乙两地的距离,根据图象中的点的实际意义即可知道,图中点B的实际意义是:4小时两车相遇.
(2)根据观察图象,可得快车所用的时间,慢车所用的时间,根据路程与时间的关系求得速度,进而求得快车从甲地驶往乙地所用的时间,然后根据待定系数法即可求得函数关系式;
(3)求得第二列快车与慢车相遇所用的时间和此时第一列快车行驶的时间,即可求得第二列快车比第一列快车晚出发的时间.
解:(1)由图象可知,甲、乙两地间的距离是900km;图中点B的实际意义是:4小时两车相遇;
故答案为:900,4小时两车相遇.
(2)慢车速度是:900÷12=75km/h,两车的速度和:900÷4=225km/h
快车速度是:225﹣75=150km/h;
相遇时慢车行驶的路程75×4=300km,
两车相遇后快车到达乙地所用的时间:300÷150=2h,
两车相遇后,2h两车行驶的路程:225×2=450km,
所以,B(4,0),C(6,450),
设线段BC的解析式为y=kx+b,
则![]() ,
,
解得![]() .
.
所以线段BC所表示的y与x之间的函数关系式为:y=225x﹣900(4≤x≤6)
(3)相遇时快车行驶的路程900﹣300=600km,
第二列快车与慢车相遇时行驶的路程:600﹣75×=562,5km,
第二列快车与慢车相遇时所用的时间:562,5÷150=3.75h,
4.5﹣3.75=0.75h.
所以,第二列快车比第一列快车晚出发0.75小时