题目内容
【题目】如图,△ ![]() 内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF
内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF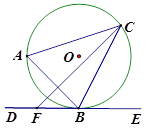
(1)求证: ![]() ;
;
(2)若⊙O 的直径为5, ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)证明:
如图:连接BO并延长交⊙O于点M,连接MC.

∴∠A=∠M,∠MCB=90°.
∴∠M+∠MBC=90°.
∵DE是⊙O的切线,
∴∠CBE+∠MBC=90°.
∴ ![]() .
.
∴ ![]() .
.
(2)解:过点 ![]() 作
作 ![]() 于点
于点 ![]() .
.
∴ ![]() .
.
由(1)得, ![]() .
.
∴ ![]() .
.
在Rt△ ![]() 中,
中,
∵ ![]() ,
,
∴ ![]() .
.
在Rt△ ![]() 中,
中,
∵ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
在Rt△ ![]() 中,
中,
∵ ![]() ,
,
∴ ![]() .
.
【解析】(1)根据圆周角定理和直径的性质,得到∠M+∠MBC=90°,再由DE是⊙O的切线,根据切线的性质,得到∠CBE=∠A;(2)由(1)得,∠M=∠CBE=∠A ,由tanA=2,根据三角函数得到tanM=tan∠CBE= tanA,根据勾股定理求出BC的值,求出CF的值.
【考点精析】本题主要考查了切线的性质定理和同角三角函数的关系(倒数、平方和商)的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;各锐角三角函数之间的关系:平方关系(sin2A+cos2A=1);倒数关系(tanAtan(90°—A)=1);弦切关系(tanA=sinA/cosA )才能正确解答此题.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】为支援四川抗震救灾,某省某市A、B、C三地分别有赈灾物资100吨、100吨、80吨,需要全部运往四川重灾区的甲、乙两县.根据灾区的情况,这批赈灾物资运往甲县的数量比运往乙县的数量的2倍少20吨.
(1)求这批赈灾物资运往甲、乙两县的数量各是多少吨?
(2)若要求C地运往甲县的赈灾物资为60吨,A地运往甲县的赈灾物资为x吨(x为整数),B地运往甲县的赈灾物资数量少于A地运往甲县的赈灾物资数量的2倍,其余的赈灾物资全部运往乙县,且B地运往乙县的赈灾物资数量不超过25吨.则A、B两地的赈灾物资运往甲、乙两县的方案有几种?
(3)已知A、B、C三地的赈灾物资运往甲、乙两县的费用如表:
A地 | B地 | C地 | |
运往甲县的费用(元/吨) | 220 | 200 | 200 |
运往乙县的费用(元/吨) | 250 | 220 | 210 |
为及时将这批赈灾物资运往甲、乙两县,某公司主动承担运送这批物资的总费用,在(2)的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?