Question

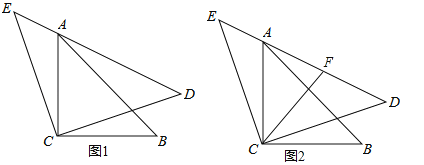
【题目】如图，在△ABC中，∠ABC和∠ACB的平分线相交于点P，根据下列条件，求∠BPC的度数．

（1）若∠ABC＝50°，∠ACB＝60°，则∠BPC＝　 　；

（2）若∠ABC+∠ACB＝120°，则∠BPC＝　 　；

（3）若∠A＝80°，则∠BPC＝　 　；

（4）从以上的计算中，你能发现已知∠A，求∠BPC的公式是：∠BPC＝　 　（提示：用∠A表示）．

Answer 1

【答案】（1）125°；（2）120°；（3）130°；（4）90°+∠A．

【解析】

（1）由∠ABC＝50°，∠ACB＝60°，∠2+∠4=25°+30°＝55°，在△BCP中，由三角形内角和为180°可得答案；

（2）同理，由ABC+∠ACB＝120°，∠ABC和∠ACB的平分线相交于点P，可得∠2+∠4＝×120°＝60°，在△BCP中，由三角形内角和为180°可得答案；

(3) A＝80°，可得ABC+∠ACB＝100°，∠2+∠4＝×100°＝50°，可得∠BPC的度数；

（4）ABC+∠ACB＝180°﹣∠A，∠ABC和∠ACB的平分线相交于点P，可得∠2+∠4＝×（180°﹣∠A），在△BCP中，∠P＝180°﹣×（180°﹣∠A）＝90°+∠A

解：（1）∵∠ABC＝50°，∠ACB＝60°，∠ABC和∠ACB的平分线相交于点P，

∴∠2+∠4＝25°+30°＝55°，

∴△BCP中，∠P＝180°﹣55°＝125°，

故答案为：125°；

（2）∵∠ABC+∠ACB＝120°，∠ABC和∠ACB的平分线相交于点P，

∴∠2+∠4＝×120°＝60°，

∴△BCP中，∠P＝180°﹣60°＝120°，

故答案为：120°；

（3）∵∠A＝80°，

∴∠ABC+∠ACB＝100°，

∠ABC和∠ACB的平分线相交于点P，

∴∠2+∠4＝×100°＝50°，

∴△BCP中，∠P＝180°﹣50°＝130°，

故答案为：130°；

（4））∵∠ABC+∠ACB＝180°﹣∠A，∠ABC和∠ACB的平分线相交于点P，

∴∠2+∠4＝×（180°﹣∠A），

∴△BCP中，∠P＝180°﹣×（180°﹣∠A）＝90°+∠A．

故答案为：90°+∠A．