题目内容
【题目】抛物线![]() 与
与![]() 轴交于A(4,0),B(6,0)两点,与
轴交于A(4,0),B(6,0)两点,与![]() 轴交于点C(0,3).
轴交于点C(0,3).
(1)求抛物线的解析式;
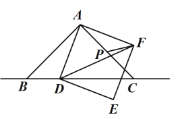
(2)点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<3).
①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时,△PDE的面积最大,并求出这个最大值;
②当t =2时,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请你求出点F的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式为: ![]() ;(2)①
;(2)①![]() ;②存在点F,使
;②存在点F,使![]() 为直角三角形;F的坐标为(5,12)或(5,2)
为直角三角形;F的坐标为(5,12)或(5,2)
【解析】试题分析:(1)根据待定系数法即可求得解析式;
(2)①依题意知:点E的坐标为E(0,t),易得直线BC的解析式为yBC=-![]() x+3,易得
x+3,易得
点D的坐标为(![]() ,
, ![]() ),从而可得
),从而可得![]() =
=![]() (
(![]() ),利用二次函数的性质即可得
),利用二次函数的性质即可得![]() 面积的最大值;
面积的最大值;
②存在点F,使![]() 为直角三角形,分情况进行讨论即可得.
为直角三角形,分情况进行讨论即可得.
试题解析:(1)抛物线![]() 与
与![]() 轴交于A(4,0),B(6,0)两点,与
轴交于A(4,0),B(6,0)两点,与![]() 轴交于点C(0,3),则有
轴交于点C(0,3),则有
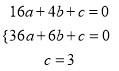 ,解得:
,解得: 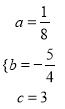 ,
,
所以抛物线的解析式为: ![]() ;
;
(2)①依题意知:点E的坐标为E(0,t),
又由点![]() ,C(0,3)易知:直线BC的解析式为yBC=-
,C(0,3)易知:直线BC的解析式为yBC=-![]() x+3,
x+3,
∵过点E的直线与![]() 轴平行交直线BC于点D,
轴平行交直线BC于点D,
∴点D的纵坐标为t,
∴当-![]() x+3=t时,
x+3=t时, ![]() ,
,
∴点D的坐标为(![]() ,
, ![]() ),
),
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴S△PDE=![]() (
(![]() ),
),
![]() ,∴
,∴![]() 的面积有最大值,
的面积有最大值,
∴当![]() 时,满足
时,满足![]() ,
,
∴![]() 的面积的最大值为
的面积的最大值为![]() ;
;
②存在点F,使![]() 为直角三角形;
为直角三角形;
理由如下:
当![]() 时,则有:P(4,0) ,
时,则有:P(4,0) , ![]() ;
;
又易知抛物线的对称轴为:直线![]() ,
,
∵点F在直线![]() 上,
上,
∴当![]() 为直角三角形时,直角顶点不可能在F处;
为直角三角形时,直角顶点不可能在F处;
则应分两种情况:
设F的坐标为(5,m), ∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
当直角顶点在E处时, ![]() ,此时可求出
,此时可求出![]() ,
,
当直角顶点在P处时, ![]() ,此时可求出
,此时可求出![]() ,
,
∴F的坐标为(5,12)或(5,2).

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】好邻居超市购进一批面粉,标准质量为![]() ,现抽取
,现抽取![]() 袋样品进行称重检测,为记录的方便,用“
袋样品进行称重检测,为记录的方便,用“![]() ”表示超过标准的重量,用“
”表示超过标准的重量,用“![]() ”表示不足标准的重量,结果如下表(单位
”表示不足标准的重量,结果如下表(单位![]() ):
):
与标准差( |
|
|
|
|
|
|
|
|
袋数 |
|
|
|
|
|
|
| 3 |
(1)求这![]() 袋样品超出或不足的质量为多少?
袋样品超出或不足的质量为多少?
(2)这批面粉的总重量为多少千克?
【题目】2017年金卉庄园“新春祈福灯会”前夕,我市某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | ... | 30 | 40 | 50 | 60 | ... |
每天销售量 | ... | 200 | 180 | 160 | 140 | ... |
(1)已知上表数据满足以下三个函数模型中的一个:①![]() ;②
;②![]() ;③
;③![]() 为常数,
为常数, ![]() 中,请你求出
中,请你求出![]() 与
与![]() 的函数关系式(不必写自变量的范围);
的函数关系式(不必写自变量的范围);
(2)求工艺厂试销该工艺品每天获得的利润![]() 与
与![]() 的函数关系式,并求当销售单价为多少时,每天获得的利润最大?最大利润是多少?
的函数关系式,并求当销售单价为多少时,每天获得的利润最大?最大利润是多少?
(3)孝感市物价部门规定,该工艺品销售单价最高不能超过72元/件,那么销售单价定为多少时,工艺厂试销工艺品每天获得的利润最大?
【题目】二次函数![]() ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
则下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
C. 二次函数的最小值是![]() D. 抛物线的对称轴是
D. 抛物线的对称轴是![]()
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果。