Question

【题目】阅读下面材料：

如图，在平面直角坐标系中，直线与双曲线交于和两点．

观察图象可知：①当或时，；②当或时，，即通过观察函数的图象，可以得到不等式的解集．

有这样一个问题：求不等式的解集．

某同学根据学习以上知识的经验，对求不等式的解集进行了探究．

下面是他的探究过程，请将（）、（）、（）补充完整：

（）将不等式按条件进行转化：

当时，原不等式不成立．

当时，原不等式可以转化为．

当时，原不等式可以转化为．

（）构造函数，画出图象．

设，，在同一坐标系中分别画出这两个函数的图象．

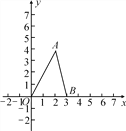
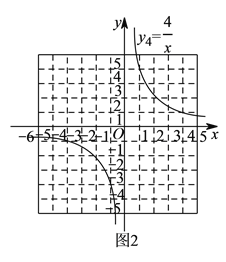
双曲线如图所示，请在此坐标系中画出抛物线．（不用列表）

（）确定两个函数图象公共点的横坐标．

观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足的所有的值为__________．

（）借助图象，写出解集．

结合（）的讨论结果，观察两个函数的图象可知：不等式的解集为__________．

Answer 1

【答案】 和． 或．

【解析】试题分析：（2）求出二次函数和反比例函数的特殊点，描点作图.(2)二次函数与反比例函数的交点就是方程的根.(3)观察图象，图象越高，函数值越大.

试题解析：

（）首先确定二次函数的对称轴，

顶点，与轴交点，

与一个交点，

即可作出二次函数的图象．

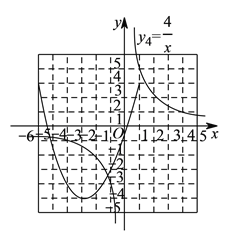
（）两个函数图象公共点的坐标是和，

则满足的所有的值为和，

故答案是：和．

（）不等式即①时，

，此时的范围是；

②当时，，

则．

故答案是：或．