题目内容
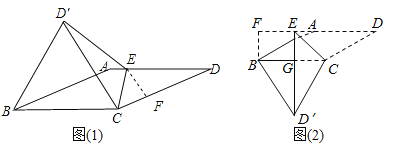
【题目】如图,四边形ABCD是平行四边形,AB=BC=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,点D的对应点为D′,连接D′B.若△D′BC为等边三角形,则DE=____________.

【答案】2![]() -2或
-2或![]() +1
+1
【解析】先判断ABCD是菱形,根据菱形的性质可得:∠D=∠ABC=30°,∠BCD=150°,然后根据△D′BC为等边三角形,可得∠BCD′=60°,然后根据折叠的性质可得:△DCE≌△D′CE,进而可得∠DCE=45°,然后过点E作EF⊥CD,垂足为F,然后解直角三角形DEF即可求出DE的值.
①如图(1)所示,当点E在边AD上时. ∵四边形ABCD是平行四边形,AB=BC=2,∴四边形ABCD是菱形.
∵AB=2,∠ABC=30°,∴CD=AB=2,∠D=∠A=30°,∠BCD=150°.
∵△D′BC为等边三角形,∴∠BCD′=60°,∴∠DCD′=90°.
∵△CDE沿CE折叠,得到△CD′E,∴△DCE≌△D′CE,∴∠DCE=![]() DCD′=45°,过点E作EF⊥CD,垂足为F,则∠CFE=90°,∴∠CEF=∠DCE=45°,∴CF=EF.在Rt△DEF中,∠D=30°,∴EF=
DCD′=45°,过点E作EF⊥CD,垂足为F,则∠CFE=90°,∴∠CEF=∠DCE=45°,∴CF=EF.在Rt△DEF中,∠D=30°,∴EF=![]() DE,设EF=x,则DE=2x,CF=x,由勾股定理可得:FD=
DE,设EF=x,则DE=2x,CF=x,由勾股定理可得:FD=![]() x.
x.
∵CF+FD=CD=2,即x+![]() =2,解得:x=
=2,解得:x=![]() ,∴DE=2x=2
,∴DE=2x=2![]() ﹣2.
﹣2.
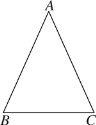
②当点E在DA的延长线上时,如图(2),过点B作BF⊥AD,交DA的延长线于点F.由折叠可知∠ED′C=∠D=30°,又∠BD′C=60°,所以D′E为∠BD′C的平分线.
又∵△BD′C是等边三角形,∴D′E⊥BC.
又∵AD∥BC,∴D′E⊥AD.
∵∠ABC=30°,∴∠BAF=30°.
又∵AB=2,∴AD=![]() ,令D′E与BC的交点为G,则易知EF=BG=
,令D′E与BC的交点为G,则易知EF=BG=![]() BC=1,
BC=1,
∴AE=![]() ﹣1,∴DE=
﹣1,∴DE=![]() +1.
+1.
故答案为:2![]() ﹣2或
﹣2或![]() +1.
+1.