题目内容
【题目】如图,在△ABC中,AB=AC.
(1)作△ABC的角平分线AD(尺规作图,保留痕迹);
(2)在AD的延长线上任取一点E,连接BE,CE.
①求证:△BDE≌△CDE;
②当AE=2AD时,四边形ABEC是平行四边形吗?请说明理由.
【答案】(1)见解析;(2) ①见解析; ②四边形ABEC是平行四边形,理由见解析.
【解析】(1)根据角平分线的作法,可得答案;
(2)①根据等腰三角形的“三线合一”可得BD=CD、∠BDE=∠CDE=90°,利用“SAS”即可判定△BDE≌△CDE;
②根据平行四边形的判定定理,可得答案.
(1)如图,线段AD即为所求;
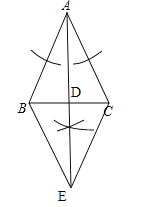
(2)①∵AB=AC,AD平分∠BAC,∴BD=CD,AD⊥BC,∴∠BDE=∠CDE=90°.
在△BDE和△CDE中,
∵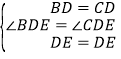
∴△BDE≌△CDE(SAS).
②∵AE=2AD,∴AD=DE.
∵BD=CD,∴四边形ABEC是平行四边形.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目