题目内容
【题目】已知在
中，
，过点
引一条射线
，
是上一点.
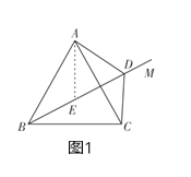
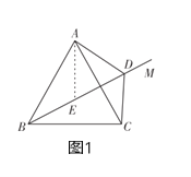
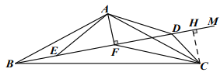
（1）如图1，
，射线在
内，
，求证：
.
请根据以下思维框图，写出证明过程.
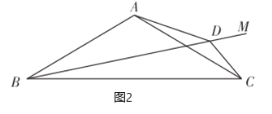
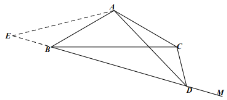
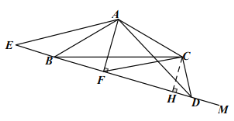
（2）如图2，已知
.
①当射线在内，求
的度数.
②当射线在
下方，请问的度数会变吗？若不变，请说明理由；若改变，请直接写出的度数.
（3）在第（2）题的条件下，作
于点
，连结
，已知
，
，求
的面积.
【答案】（1）见解析；（2）①
；②会变，
；（3）
或
.
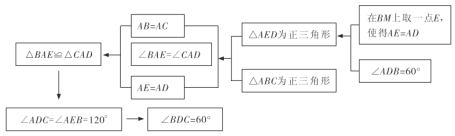
【解析】
(1)根据SAS可证明 
，再利用三角形内角和即可得求证
的度数为60°；
（2）①在
上取一点
，
，根据SAS可证明，再利用三角形内角和即可得求得的度数；
②在
延长线上取一点，使得，根据SAS可证明，再利用三角形内角和即可得求得的度数，与①进行比较即可得出答案；
（3）分当射线
在
内：作
，可得△DCH是30°的直角三角形，可得CH的长度，即可得出△CDF的面积. 当射线在
下方:由等腰三角形AED的性质可得
，即可得出△CDF的面积.
解：（1）在上取一点，使.
，
是等边三角形.
，
，
是正三角形，
，
，
，
.
（2）①在上取一点，，
，且
，
，
，
，
，
，
，
.
②会变.
在延长线上取一点，使得，
同理可得：，
，
.
（3）当射线在内,如图，
，
且，
，
，
作，
，
，
，
，
，
当射线在下方:如图，
，
且，，
.
，
.
练习册系列答案
名校课堂系列答案
相关题目
