Question

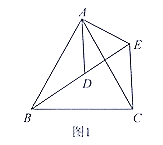
【题目】(1)问题发现:如图1, 和均为等边三角形，点在同一直线上，连接

①求证:; ②求的度数.

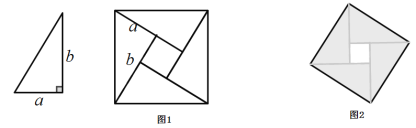
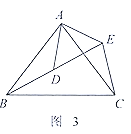
(2)拓展探究:如图2, 和均为等腰直角三角形，,点在同一直线上为中边上的高，连接

①求的度数:

②判断线段之间的数量关系(直接写出结果即可).

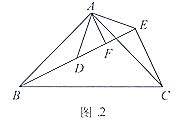
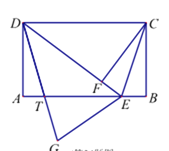
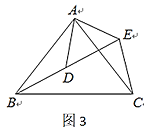
解决问题:如图3，和均为等腰三角形，,点在同一直线上，连接.求的度数(用含的代数式表示，直接写出结果即可).

Answer 1

【答案】（1）①证明见解析；②60°；（2）①90°；②BE=CE+2AF；（3）∠AEC=90°+.

【解析】

（1）根据等边三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=60°,根据SAS进一步证明△BAD≌△CAE,依据其性质可得，再根据对应角相等求出的度数；

（2）根据等腰直角三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=90°，根据SAS进一步证明△BAD≌△CAE，根据对应角相等求出的度数；因为DE=2AF,BD=EC,结合线段的和差关系得出结论；

（3）根据等腰三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=n°，根据SAS进一步证明△BAD≌△CAE，根据对应角相等求出得出∠ADB=的度数,结合内角和用n表示∠ADE的度数，即可得出结论.

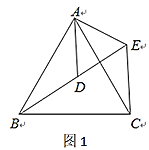
（1）①∵△ABC和△ADE均为等边三角形(如图1)，

∴ AB=AC，AD=AE，∠BAC=∠DAE=60°，

∴ ∠BAC-∠DAC=∠DAE-∠DAC，

∴ ∠BAD=∠CAE.

∴ △BAD≌△CAE（SAS）

∴ BD=CE.

② 由△CAE≌△BAD，

∴ ∠AEC=∠ADB=180°-∠ADE=120°.

∴ ∠BEC=∠AEC-∠AED=120°-60°=60°.

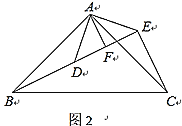
（2）①∵△ABC和△ADE均为等腰直角三角形(如图2)，

∴ AB=AC，AD=AE，∠ADE=∠AED=45°，

∵ ∠BAC=∠DAE=90°，

∴ ∠BAC-∠DAC=∠DAE-∠DAC，

∴ ∠BAD=∠CAE.

∴ △BAD≌△CAE（SAS）.

∴ BD=CE，∠AEC=∠ADB=180°-∠ADE=135°.

∴ ∠BEC=∠AEC-∠AED=135°-45°=90°.

② BE=CE+2AF.

（3）如图3：∠AEC=90°+，理由如下，

∵△ABC和△ADE均为等腰直角三角形，

∴ AB=AC，AD=AE，∠ADE=∠AED=n°，

∴ ∠BAC-∠DAC=∠DAE-∠DAC，

∴ ∠BAD=∠CAE.

∴ △BAD≌△CAE（SAS）.

∴ ∠AEC=∠ADB=180°-∠ADE=180°- .

∴∠AEC=90°+.