��Ŀ����
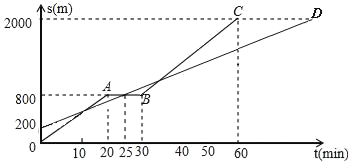
����Ŀ��С���ͰְִӼҲ���ȥ�����ְ��ȳ���һֱ����ǰ�У�С�����������ǰ�У���;����Ϣһ��ʱ��������ԭ��ǰ�У��ҵ����ľ���Ϊ2000m����ͼ��С���Ͱְ����ߵ�·��S��m���벽��ʱ��t��min���ĺ���ͼ��
��1��ֱ��д��BC��ͼ������Ӧ�ĺ�����ϵʽ������д��t��ȡֵ��Χ����
��2��С����������ʱ����ְֵ�����������
��3�����ٶȶ����������£�С��ϣ���Ȱְ���18���ӵ��﹫����С���ڲ��й�����ͣ����ʱ��������� �����ӣ�
���𰸡���1��s=40t��400����2��37.5min; ��3��3��
�����������������
�����������1���۲�ͼ����BC�����ĵ� �����ô���ϵ�������.��2�����������飬���.(3)���С���ְֵ����ʱ�䣬�����С���ڲ��й�����ͣ����ʱ��.
�⣺��1����ֱ��BC����Ӧ�ĺ�������ʽΪs=kt+b��
����30��800������60��2000�������,
![]() ,
,
���![]() ,
,
��ֱ��BC����Ӧ�ĺ�������ʽΪs=40t��400.
��2����С���İְ�����·��s��ʱ��t�ĺ�����ϵʽ��s=mt+n��
��![]() �����
�����![]() .
.
��С���İְ�����·��s��ʱ��t�ĺ�����ϵʽ��s=24t+200��
�ⷽ����![]() ����
����![]() ��
��
��С������37.5minʱ��ְֵ���������.
��3����s=2000ʱ��2000=24t+200����t=75��
��75��60=15��
��С��ϣ���Ȱְ���18min���﹫����С���ڲ��й�����ͣ����ʱ����Ҫ����3min��
�ʴ�Ϊ3��

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�