Question

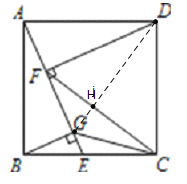
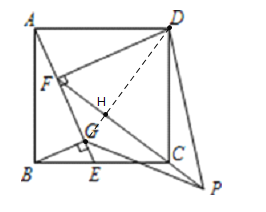
【题目】如图，正方形ABCD中，E为BC边上一点，DF⊥AE于F，BG⊥AE于G．

（1）求证：DF=BG＋FG．

（2）连接FC，CG，若四边形DCGF的面积为40，求FC的长．

（3）在（2）的条件下，若AG=7，P为FC的延长线上任一点，连PD、PG，直接写出的值为___．

Answer 1

【答案】（1）见解析；（2）FC长为；（3）18

【解析】

（1）先证∠BAG=∠ADF，再证△BAG≌△ADF即可；

（2）连接DG，交CF于点H，先证∠DAF=∠FDC，再证△ADG≌△DCF，得到DG=CF，DG⊥CF，再根据四边形DCGF的面积为40，求出FC的长即可；

（3）连接DG，交CF于点H，先求出FG的长，再证，即可求出其值.

解：（1）∵DF⊥AE，BG⊥AE，

∴∠DFA=∠AGB=90°，

∵四边形ABCD为正方形，

∴∠BAD=90°，AB=AD，

∴∠DAF+BAG=90°，∠DAF+∠ADF=90°，

∴∠BAG=∠ADF，

在△BAG和△ADF中

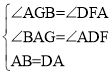
∴△BAG≌△ADF（AAS），

∴AG=DF，BG=AF，

∴DF=BG+FG；

（2）连接DG，交CF于点H，

∵∠ADC=90°，

∴∠ADF+∠FDC=90°，

∵∠DAF+∠ADF=90°，

∴∠DAF=∠FDC，

在△ADG和△DCF中

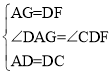
∴△ADG≌△DCF（SAS），

∴DG=CF，∠AGD=∠DFC，

∵∠DFE=90°，

∴∠DFC+∠HFG=90°，

∴∠AGD+∠HFG=90°，

∴∠FHG=90°，

∴ DG⊥CF，

∵四边形DCGF的面积为40，

∴，

解得：或（舍去），

则FC长为；

（3）连接DG，交CF于点H，

∵AG=7，

∴DF=AG=7,

由（2）知DG=CF=，

∴在Rt△DFG中，

，

∵DG⊥CF，

∴在Rt△DHP中，

，

在Rt△GHP中，

，

∴，

在Rt△DHF中，

，

在Rt△GHF中，

，

∴，

∴.