Question

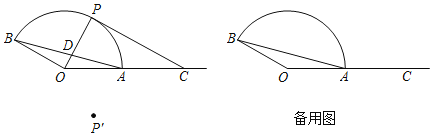
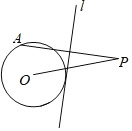
【题目】如图，⊙O的半径为4，点P是⊙O外的一点，PO=10，点A是⊙O上的一个动点，连接PA，直线l垂直平分PA，当直线l与⊙O相切时，PA的长度为____________．

Answer 1

【答案】．

【解析】

如图设切点为E，作OF⊥PA于F，连接OE．直线l交PA于K，则四边形OEKF是矩形．设AK=PK=x，由OE=KF=4，推出AF=x﹣4，PF=x+4，由OF2=OA2﹣AF2=OP2﹣PF2，列出方程即可解决问题．

如图设切点为E，作OF⊥PA于F，连接OE．

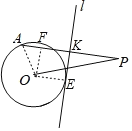
直线l交PA于K，则四边形OEKF是矩形．

设AK=PK=x．

∵OE=KF=4，

∴AF=x﹣4，PF=x+4．

在中，

∵OF2=OA2﹣AF2=OP2﹣PF2，

∴42﹣(x﹣4)2=102﹣(x+4)2，

∴x，

∴PA=2x．

故答案为：．