题目内容
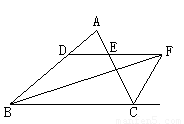
如图所示：∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E．
问：（1）图中有几个等腰三角形？为什么？
（2）BD，CE，DE之间存在着什么关系？请证明．
【答案】
（1）图中等腰三角形有△BDF，△CEF。 2′
∵BF平分∠ABC，∴∠DBF=∠CBF，∵DF∥BC，∠FBC=∠DFB，
∴∠DBF=∠DFB，∴△DBF是等腰三角形； 4′
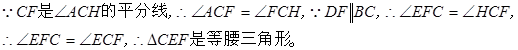6′
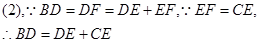8′
【解析】（1）根据已知条件，BF、CF分别平分∠ABC、∠ACB的外角，且DE∥BC，可得∴∠DBF=∠DFB，∠ECF=∠EFC，因此可判断出△BDF和△CEF为等腰三角形；
（2）由（1）可得出DF=BD，CE=EF，所以得BD-CE=DE．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
（2012•内江）如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为（ ）
如图所示，△ABC的三个顶点的坐标分别为A（4，3）、B（-2，1）、C（0，-1），则△ABC外接圆的圆心坐标是
如图所示为△ABC的各边，角的数据．利用全等三角形的条件，从中选取适当的数据，画出与△ABC全等的三角形，则方法共有（ ）
如图所示三角形ABC的面积为（ ）cm2．
如图所示，△ABC的顶点坐标分别是A（0，0）、B（6，0）、C（5，5）．