题目内容
 如图所示,△ABC的三个顶点的坐标分别为A(4,3)、B(-2,1)、C(0,-1),则△ABC外接圆的圆心坐标是
如图所示,△ABC的三个顶点的坐标分别为A(4,3)、B(-2,1)、C(0,-1),则△ABC外接圆的圆心坐标是(1,2)
(1,2)
;△ABC外接圆的半径为| 10 |
| 10 |
分析:求出AB、AC、BC,根据勾股定理的逆定理得出∠ACB=90°,根据A、B的坐标求出即可.
解答:解:∵A(4,3)、B(-2,1)、C(0,-1),
∴AB2=(4+2)2+(3-1)2=40,AC2=(4-0)2+(3+1)2=32,BC2=(-2-0)2+(1+1)2=8,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵AB=
=2
,
∴△ABC的外接圆的半径是
×2
=
,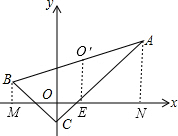
过B作BM⊥x轴于M,过A作AN⊥x轴于N,过O′作O′E⊥x轴于E,
∵A(4,3)、B(-2,1),
∴BM=1,AN=3,MN=4+2=6,BM∥O′E∥AN,
∵O′为AB中点,
∴E为MN中点,
∴O′E=
×(BM+AN)=2,EN=
MN=3,
∴OE=4-3=1,
即O′的坐标是(1,2),
故答案为:(1,2),
.
∴AB2=(4+2)2+(3-1)2=40,AC2=(4-0)2+(3+1)2=32,BC2=(-2-0)2+(1+1)2=8,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵AB=
| 40 |
| 10 |
∴△ABC的外接圆的半径是
| 1 |
| 2 |
| 10 |
| 10 |

过B作BM⊥x轴于M,过A作AN⊥x轴于N,过O′作O′E⊥x轴于E,
∵A(4,3)、B(-2,1),
∴BM=1,AN=3,MN=4+2=6,BM∥O′E∥AN,
∵O′为AB中点,
∴E为MN中点,
∴O′E=
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=4-3=1,
即O′的坐标是(1,2),
故答案为:(1,2),
| 10 |
点评:本题考查了勾股定理的逆定理,梯形的中位线,三角形的外接圆与外心等知识点的应用,注意:直角三角形的外接圆的圆心在斜边的中点上,半径等于斜边的一半.

练习册系列答案
相关题目
 (2012•内江)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
(2012•内江)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( ) 如图所示为△ABC的各边,角的数据.利用全等三角形的条件,从中选取适当的数据,画出与△ABC全等的三角形,则方法共有( )
如图所示为△ABC的各边,角的数据.利用全等三角形的条件,从中选取适当的数据,画出与△ABC全等的三角形,则方法共有( ) 如图所示三角形ABC的面积为( )cm2.
如图所示三角形ABC的面积为( )cm2. 如图所示,△ABC的顶点坐标分别是A(0,0)、B(6,0)、C(5,5).
如图所示,△ABC的顶点坐标分别是A(0,0)、B(6,0)、C(5,5).