题目内容
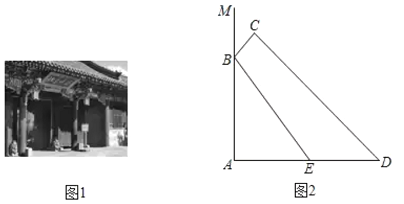
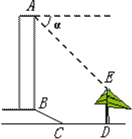
【题目】如图所示，某校教学楼正前方有一棵大树DE，高度是10米，从教学楼顶端A测得大树顶端E的俯角α是45°，大树低端D到教学楼前台阶底边的水平距离CD是15米，台阶坡长BC是6米，台阶的坡度i=1：
，求教学楼AB的高度约为多少米？（结果精确到0.1米，参考数据：
）
【答案】教学楼AB的高约为27.2米
【解析】
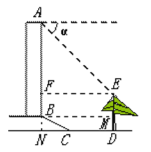
过E作EF⊥AB于F，过B作BM⊥DE于M，延长AB交CD于N，根据勾股定理求得BN，CN，再分别求出AF、BF的长，即可求得教学楼AB的高．
如图，过E作EF⊥AB于F，过B作BM⊥DE于M，延长AB交CD于N，
∵i=1：
，BC=6，设BN=
，则CN=
，
由题意有
，即
，
解得
，（-3舍去）
∴BN=DM
，CN
，
∵DE=10，α=45°，CD=15，
∴AF=EF=BM=DN=DC+CN=15+
，BF=ME=DE-DM=10-3=7．
∴AB=AF+BF=22+≈27.2（米）．
即教学楼AB的高约为27.2米．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
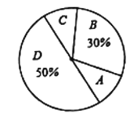
【题目】研究机构对本地区18－20岁的大学生就某个问题做随机调查，要求被调查者从A、B、C、D四个选项中选择自己赞同的一项，并将结果绘制成两幅不完整的统计图(如图)：
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题：
(1)m＝_____，b＝_____．
(2)若该地区18~20岁的大学生有1.2万人，请估计这些大学生中选择赞同A选项的人数：
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈，而选择“C”的这4人中只有一名男性，求这名男性刚好被抽取到的概率．
