Question

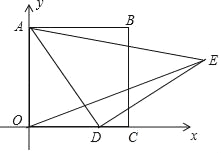
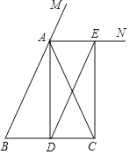
【题目】已知：如图，在△ABC中，AB＝AC，AD是△ABC的中线，AN为△ABC的外角∠CAM的平分线，CE∥AD，交AN于点E．求证：四边形ADCE是矩形．

Answer 1

【答案】见解析

【解析】

由在△ABC中，AB=AC，AD是BC边的中线，可得AD⊥BC，∠BAD=∠CAD，又由AN为△ABC的外角∠CAM的平分线，可得∠DAE=90°，又由CE⊥AN，可得∠AEC＝∠DCE=90°，即可证得：四边形ADCE为矩形；

∵在△ABC中，AB＝AC，AD是BC边的中线，

∴AD⊥BC，∠BAD＝∠CAD，

∴∠ADC＝90°，

∵AN为△ABC的外角∠CAM的平分线，

∴∠MAN＝∠CAN，

∴∠BAD+∠CAD+∠MAN+∠CAN=180°，

∴∠DAE＝∠CAD+∠CAN=×180°=90°，

∵CE//AD，

∴CE⊥AN，

∴∠AEC＝∠DCE=90°，

∴四边形ADCE为矩形．