题目内容
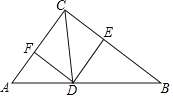
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是∠ACB的平分线,交AB于点D,过点D分别作AC、BC的平行线DE、DF,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D. 四边形DECF是正方形
D. 四边形DECF是正方形
【答案】A
【解析】
(1)![]() 是
是![]() 的平分线,证不到D是AB的中点;
的平分线,证不到D是AB的中点;
(2)根据平分线和平行和条件可以证明![]() ;
;
(3)根据![]() 是
是![]() 的平分线可证得;
的平分线可证得;
(4)首先根据题意可得四边形DECF是平行四边形,然后再证明FC=DF,根据邻边相等的平行四边形可得四边形DECF是菱形,再由∠ACB=90°,根据有一个角是直角的菱形是正方形可得菱形DECF是正方形.
解∵过D点分别作AC和BC的平行线,交BC于点E,交AC于点F,
∴DE∥AC,DF∥BC,
∴四边形DECF是平行四边形,
又∵AD平分∠ACB,
∴∠BCD=∠ACD,
∵DF∥BC,
∴∠FDC=∠BCD,
∴∠ACD=∠FDC,
∴FC=DF
∴四边形DECF为菱形,
又∠ACB=90°时,
∴菱形DECF是正方形.
综上所述可知FC=DF、∠BCD=∠ACD、四边形DECF是正方形是正确的,AD=BD是错误的。
故选:A.

【题目】八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | a | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
请解答以下问题:
(1)频数分布表中a= ,把频数分布直方图补充完整;
(2)求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该居委会有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?

【题目】为了解全区3000名九年级学生英语听力口语自动化考试成绩的情况,随机抽取了部分学生的成绩(满分30分且得分均为整数),制成下表:
分数段(x分分) | 0≤x≤18 | 19≤x≤21 | 22≤x≤24 | 25≤x≤27 | 28≤x≤30 |
人数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数所在的分数段是 ;
③若用扇形统计图表示统计结果,则分数段为0≤x≤18的人数所对应扇形的圆心角为 °;
(2)如果将25分以上(含25分)定为优秀,请估计全区九年级考生成绩为优秀的人数.