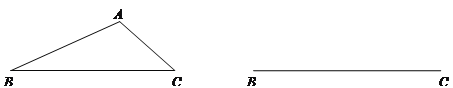Question

【题目】（1）观察发现：如图1，在中，，点在边上，过作交于，，，．填空：

①与是否相似（直接回答）________；

②________；________；

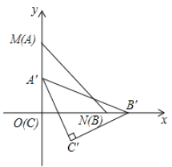
（2）拓展探究：将绕顶点旋转到图2所示的位置，猜想与是否相似？若不相似，说明理由；若相似，请证明；

（3）迁移应用：将绕顶点旋转到点、、在同一条直线上时，直接写出线段的长．

Answer 1

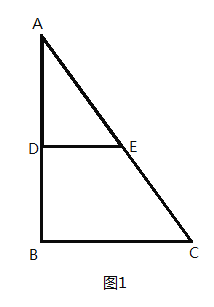
【答案】（1）①相似；② ，；（2），证明见解析；（3）或．

【解析】

（1）①根据即可得到相似的结论；

②根据相似的性质列比例线段即可得到答案；

（2）相似，根据两组边成比例夹角相等即可证明；

（3）分别画出图形，根据勾股定理求出BD，即可得到答案.

解：（1）①∵，

∴与相似，

故答案为：相似；

②∵， ,

∴∠ADE=90°，

∵，,

∴,

∵∽，

∴,

∵，，,

∴AE=,

故答案为：，；

（2），

理由如下：由旋转变换的性质可知，，

由（1）得，，又，

∴；

（3）如图2，在中，，

∵点、、在同一条直线上，

∴，

如图3，，

线段的长为或．

综上所述，将绕顶点旋转到点、、在同一条直线上时，线段的长为或．