题目内容
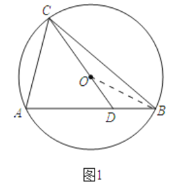
【题目】如图,已知△ABC内接于⊙O,延长CO交AB于点D,记∠A=![]() ,∠ABC=β.
,∠ABC=β.
(1)求∠ADC的度数(用含α、β的式子表示);
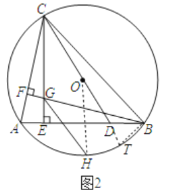
(2)过点C作CE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F,CE,BF相交于点G,取![]() 中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.
中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.

【答案】(1)![]() ;(2)①证明见解析;②证明见解析.
;(2)①证明见解析;②证明见解析.
【解析】
(1)根据∠CDA=∠DCB+∠ABC,只要求出∠DCB即可解决问题.
(2)①延长CD交⊙O于T,连接BT,OH.根据CT是直径,可得∠AEC=∠BFC=∠CBT=90°,根据等量关系可得∠FCG=∠BCT,然后可得△CFG∽△CBT,根据α+β=120°可得∠ACB=60°,然后求出∠CBF=30°,根据相似的性质求出CG=![]() CT =CO;
CT =CO;
②根据垂弦定理得出OH⊥AB,已知CE⊥AB,可得CG∥OH,推出四边形CGHO是平行四边形即可解决问题.
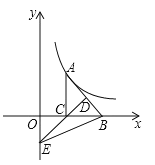
(1)解:如图1中,连接OB,
∵∠BOC=2∠A=2![]() ,OC=OB,
,OC=OB,
∴∠OCB=![]() (180°-2
(180°-2![]() )=90°-
)=90°-![]() ,
,
∴∠ADC=∠OCB+∠ABC=![]() .
.
(2)证明:如图2,延长CD交⊙O于T,连接BT,OH.
①∵CT是直径,
∴∠CBT=90°,
∵CE⊥AB,BF⊥AC,
∴∠AEC=∠BFC=∠CBT=90°,
∴∠A+∠ACE=90°,∠T+∠BCT=90°,
∵∠A=∠T,
∴∠FCG=∠BCT,
∵α+β=120°,
∴∠ACB=60°,
∴∠CBF=30°,
∴BC=2CF,
∵∠FCG=∠BCT,∠CFG=∠CBT=90°,
∴△CFG∽△CBT,
∴![]() =2,
=2,
∴CG=![]() CT=OC=OT=OH,
CT=OC=OT=OH,
②∵![]() ,
,
∴OH⊥AB,
∵CE⊥AB,
∴CE∥OH,∵CG=OH,
∴四边形CGHO是平行四边形,
∴GH∥CD.

【题目】某小型加工厂准备每天生产甲、乙两种类型的产品共1000件,原料成本、销售单价,及工人计件工资如表:
甲(元/件) | 乙(元/件) | |
原料成本 | 10 | 8 |
销售单价 | 20 | 16 |
计件工资 | 2 | 1.5 |
设该加工厂每天生产甲型产品x件,每天获得总利润为y元.
(1)求出y与x之间的函数关系式;
(2)若该工厂每天投人总成本不超过10750元,怎样安排甲、乙两种类型的生产量,可使该厂每天所获得的利润最大?并求出最大利润.(总成本=原料成本+计件工资,利润=销售收入一投人总成本)