��Ŀ����
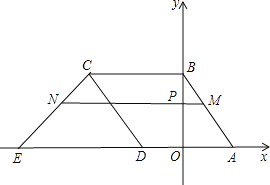
����Ŀ��ֱ��![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
����ֱ��д����C����D�����꣬�����m��ֵ��
����P��0��t�����߶�OB�ϵ�һ�����㣨��P����O��B�غϣ���������P��ƽ����x���ֱ�߽�AB��M����CE��N�����߶�MN�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д�Ա�����ȡֵ��Χ����
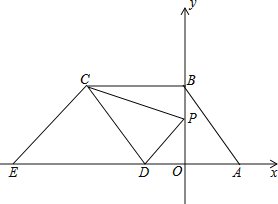
����P��0��t����y���������ϵ�һ�����㣬Ϊ��ֵʱ��P��C��Dǡ�������һ�����������Σ�
���𰸡���1��m=9����2��![]() ����3��t=4����t=
����3��t=4����t=![]() ��t=
��t=![]() ʱ����PCD��Ϊ����������.
ʱ����PCD��Ϊ����������.
��������
������1����ֱ�ߵĽ���ʽ�����A��B������꣬�ٸ������ε����ʼ��������C����D�����꣬�ѵ�C���������ֱ��y=x+m�������m��ֵ��
��2�����M������Ϊ��xM��t������N������Ϊ��xN��t�����������xM=��![]() t+3�������xN=t��9�������õ�d=xM��xN=��
t+3�������xN=t��9�������õ�d=xM��xN=��![]() t+3����t��9��=��
t+3����t��9��=��![]() t+12��
t+12��
��3����A��B����������AB�ij����ٷ���������ֱ�����������������tֵ���ɣ�
�����������1����ֱ��y=��![]() x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��
x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��
����A��������3��0����B��������0��4����
���ı���ABCD�����Σ�
����C����������5��4������D����������2��0����
��ֱ��y=x+m������C��
��m=9��
��2����MN ������P��0��t����ƽ����x�ᣬ
�������M��������xM��t������N��������xN��t����
����M��ֱ��AB�ϣ�
ֱ��AB�Ľ���ʽΪy=��![]() x+4��
x+4��
��t=![]() ����xM=��
����xM=��![]() t+3��
t+3��
ͬ����N��ֱ��CE�ϣ�ֱ��CE�Ľ���ʽΪy=x+9��
��t=xN+9����xN=t��9��
��MN��x�����߶�MN�ij���Ϊd��
��d=xM��xN=��![]() t+3����t��9��=��
t+3����t��9��=��![]() t+12��
t+12��
��3����ֱ��AB�Ľ���ʽΪy=��![]() x+4��
x+4��
����A ��������3��0������B��������0��4����AB=5��
���ı���ABCD�����Σ�
��AB=BC=CD=5��
����P�˶�����Bʱ����PCD��Ϊ��BCD��һ�����������Σ���ʱ=4��
����P��0��t����y���������ϵ�һ�����㣬
��OP=t��PB=|t��4|��
����D����������2��0����
��OD=2���ɹ��ɶ�����PD2=OD2+OP2=4+t2��
ͬ����CP2=BC2+BP2=25+��t��4��2��
��PD=CD=5ʱ��PD2=4+t2=25��
��t=![]() ���Ḻ����
���Ḻ����
��PD=CPʱ��PD2=CP2��4+t2=25+��t��4��2��
��t=![]() ��
��
����������t=4����t=![]() ��t=
��t=![]() ʱ����PCD��Ϊ���������Σ�
ʱ����PCD��Ϊ���������Σ�

 ��У����ϵ�д�
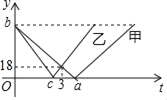
��У����ϵ�д�����Ŀ��������������Ӱ������������������ڽ��꺮���ڼ䣬ijУ���꼶һ����ۺ�ʵ��С��ѧ���ԡ�������������Ҫ����������������ڳ��в��������Ե�������������������������ͼ��ʾ�IJ�������ͳ��ͼ����
��� | ������������Ҫ���� | �ٷֱ� |
A | ��ҵ��Ⱦ | 45% |
B | ����β���ŷ� |
|
C | ¯�����ŷ� | 15% |
D | �������Ŀ��ķ��ȣ� |
|
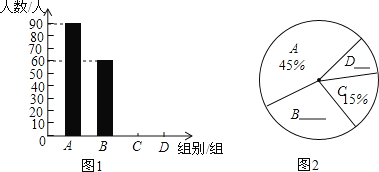
�����ͳ��ͼ���ش��������⣺
��1�����α�����������ж����ˣ�����![]() ��
��![]() ��ֵ��
��ֵ��
��2���벹ȫ����ͳ��ͼ������������ͳ��ͼ����������![]() ����Ӧ��Բ�ĽǵĶ�����
����Ӧ��Բ�ĽǵĶ�����
��3����������100���˿ڣ������������Ϊ����ҵ��Ⱦ������β���ŷ�������������Ҫ��������.