题目内容
【题目】如图,O为∠MBN角平分线上一点,⊙O与BN相切于点C,连结CO并延长交BM于点A,过点A作AD⊥BO于点D.
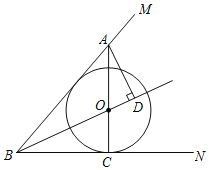
(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
【答案】(1)见解析;(2)AD=2![]() .
.
【解析】
(1)作OE⊥AB,先由∠AOD=∠BAD求得∠ABD=∠OAD,再由∠BCO=∠D=90°及∠BOC=∠AOD求得∠OBC=∠OAD=∠ABD,最后证△BOC≌△BOE得OE=OC,依据切线的判定可得;
(2)先求得∠EOA=∠ABC,在Rt△ABC中求得AC=8,AB=10,由切线长定理知BE=BC=6,AE=4,OE=3,继而得BO=3![]() ,根据相似三角形的性质即可得出结论.
,根据相似三角形的性质即可得出结论.
解:(1)过点O作OE⊥AB于点E,
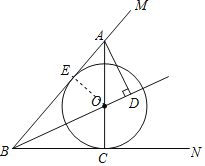
∵O为∠MBN角平分线上一点,
∴∠ABD=∠CBD,
又∵BC为⊙O的切线,
∴AC⊥BC,
∵AD⊥BO于点D,
∴∠D=90°,
∴∠BCO=∠D=90°,
∵∠BOC=∠AOD,
∴∠BAD+∠ABD=90°,∠AOD+∠OAD=90°,
∵∠AOD=∠BAD,
∴∠ABD=∠OAD,
∴∠OBC=∠OAD=∠ABD,
在△BOC和△BOE中,
∵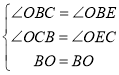 ,
,
∴△BOC≌△BOE(AAS),
∴OE=OC,
∵OE⊥AB,
∴AB是⊙O的切线;
(2)∵∠ABC+∠BAC=90°,∠EOA+∠BAC=90°,
∴∠EOA=∠ABC,
∵tan∠ABC=![]() 、BC=6,
、BC=6,
∴AC=BCtan∠ABC=8,
则AB=10,
由(1)知BE=BC=6,
∴AE=4,
∵tan∠EOA=tan∠ABC=![]() ,
,
∴![]() ,
,
∴OE=3,OB=![]() =3
=3![]() ,
,
∵∠ABD=∠OBC,∠D=∠ACB=90°,
∴△ABD∽△OBC,
∴![]() ,即
,即![]() ,
,
∴AD=2![]() .
.
故答案为:AD=2![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.