题目内容
【题目】下面的方格纸中,画出了一个“小老鼠”的图案,已知每个小正方形的边长为1
(1)在上面的方格纸中作出“小老鼠”关于直线DE对称的图案(只画图,不写作法).
(2)以G为原点,GE所在直线为x轴,GH所在直线为y轴,小正方形的边长为单位长度建立直角坐标系,问:是否存在以点Q为顶点,且过点H和E的抛物线,并通过计算说明理由?

【答案】(1)答案见解析;(2)不存在以点Q为顶点,同时又经过点H和点E的抛物线,理由见解析.
【解析】
(1)利用轴对称的性质作出对称图形即可;
(2)求出以Q为顶点,过点H的抛物线的解析式,再判断点E是否在抛物线上即可.
解:(1)“小老鼠”关于直线DE对称的图案如图所示:
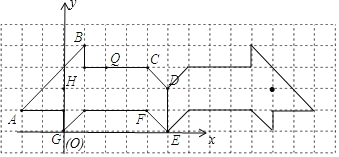
(2)建立坐标系后:H(0,2),Q(2,3),E(5,0)
假设存在这样的抛物线:
设函数式为:y=a(x﹣2)2+3,
∵H在抛物线上,所以把x=0,y=2代入抛物线得:2=4a+3,
∴a![]() ,
,
∴函数表达式是:y![]() (x﹣2)2+3,
(x﹣2)2+3,
若点E在抛物线上,则x=5时,y=0;
把x=5,代入抛物线有:y![]() (5﹣2)2+3
(5﹣2)2+3![]() 0,
0,
∴点E不在抛物线上,
∴不存在以点Q为顶点,同时又经过点H和点E的抛物线.

练习册系列答案
相关题目