题目内容
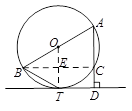
如图,AB为⊙O的直径,直线DT切⊙O于T,AD⊥DT于D,交⊙O于点C,AC=2,DT =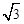 ,求∠ABT的度数.
,求∠ABT的度数. 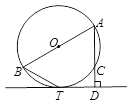
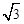 ,求∠ABT的度数.
,求∠ABT的度数. 
60°
试题分析:连接OT、BC,相交于点E,根据切线的性质可得∠OTD=90°,再根据圆周角定理结合AD⊥DT可证得四边形CDTE是矩形,即可得到∠CET=90°,
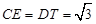 ,根据垂径定理可得
,根据垂径定理可得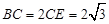 ,从而可得∠ABC=30°,再结合OB=OT可得△OBT为等边三角形,从而可以求得结果.
,从而可得∠ABC=30°,再结合OB=OT可得△OBT为等边三角形,从而可以求得结果.连接OT、BC,相交于点E
∵直线DT切⊙O于T
∴∠OTD = 90°
∵AD⊥DT于D
∴∠ADT = 90°
∵AB为⊙O的直径
∴∠ACB = 90°
∴∠DCB = 90°
∴四边形CDTE是矩形
∴∠CET=90°,
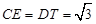 .
.∴
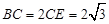
∵
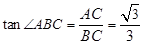
∴∠ABC=30°
∴∠BOT=60°
∵OB="OT"
∴△OBT为等边三角形.
∴∠ABT=60°.
点评:解答本题的关键是熟练掌握切线垂直于经过切点的半径,直径所对是圆周角是直角,有一个角是60°的等腰三角形的等边三角形.

练习册系列答案
相关题目
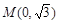 为圆心,以
为圆心,以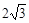 长为半经作圆M交
长为半经作圆M交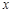 轴于A,B两点,连结AM并延长交圆M于点P,连结PC交轴于点E。
轴于A,B两点,连结AM并延长交圆M于点P,连结PC交轴于点E。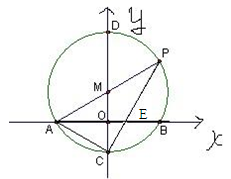
 的直径CD与弦AB交于点M,添加一个条件 , 得到M是AB的中点。
的直径CD与弦AB交于点M,添加一个条件 , 得到M是AB的中点。
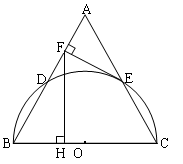


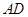 ∶
∶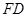 =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长. 为⊙O的四等分点,动点
为⊙O的四等分点,动点 从圆心
从圆心 出发,沿
出发,沿 路线作匀速运动,设运动时间为
路线作匀速运动,设运动时间为 (s).
(s). ,则下列图象中表示
,则下列图象中表示 与
与
 cm2
cm2