题目内容
圆内接正六边形边长为6,则该圆的内接正三角形边长为( )
A、6
| ||
B、9
| ||
C、6
| ||
| D、12 |
考点:正多边形和圆
专题:计算题
分析:根据题意画出图形,设出圆的半径,再由正多边形及直角三角形的性质求解即可.
解答: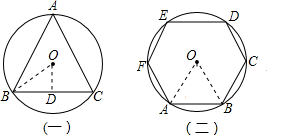 解:如图(二),
解:如图(二),
∵圆内接正六边形边长为6,
∴AB=6,
可得△OAB是等边三角形,圆的半径为6,
∴如图(一),
连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB•cos30°=
×6=3
,
故BC=2BD=6
.
故选:A.
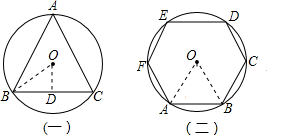 解:如图(二),
解:如图(二),∵圆内接正六边形边长为6,
∴AB=6,
可得△OAB是等边三角形,圆的半径为6,
∴如图(一),
连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB•cos30°=
| ||
| 2 |
| 3 |
故BC=2BD=6
| 3 |
故选:A.
点评:本题考查的是圆内接正三角形及正六边形的性质,根据题意画出图形,作出辅助线构造出直角三角形是解答此题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于( )
如图,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于( )| A、48 | B、24 | C、8 | D、16 |
一个圆心角为120°的扇形的弧长为4π,则该扇形的面积为( )
| A、6π | B、12π |
| C、18π | D、24π |
到△ABC的三个顶点距离相等的点是△ABC( )的交点.
| A、三边中线 |
| B、三条角平分线 |
| C、三边上高 |
| D、三边垂直平分线 |
菱形具有而矩形不具有的性质是( )
| A、两条对角线相等 |
| B、两条对角线互相平分 |
| C、两条对角线互相垂直 |
| D、既是轴对称图形又是中心对称图形 |
若点(x,y)关于y轴的对称点在第二象限,则x和y的符号是( )
| A、x<0,y>0 |
| B、x>0,y>0 |
| C、x<0,y<0 |
| D、x>0,y<0 |
 如图,下面推理正确的是( )
如图,下面推理正确的是( )| A、∵∠1=∠3,∴AD∥BC |
| B、∵∠A+∠1+∠2=180°,∴AD∥BC |
| C、∵∠A+∠3+∠4=180°,∴AB∥CD |
| D、∵∠2=∠4,∴AD∥BC |