题目内容
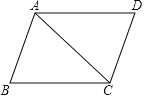
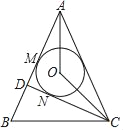
【题目】如图,AB=AC,CD⊥AB于点D,点O是∠BAC的平分线上一点,⊙O与AB相切于点M,与CD相切于点N
(1)求证:∠AOC=135°;
(2)若NC=3,BC=2![]() ,求DM的长.
,求DM的长.
【答案】(1)∠AOC=135°;(2)DM=1.
【解析】
(1)如图,作OE⊥AC于E,连接OM,ON,由切线的性质可得OM⊥AB,ON⊥CD,由角平分线的性质可得OM=OE,从而得AC是⊙O的切线,继而可得OC平分∠ACD,继而通过推导即可证得∠AOC=135°;
(2)由切线长定理可得AM=AE,DM=DN,CN=CE=3,设DM=DN=x,AM=AE=y,则有BD=3﹣x,在Rt△BDC中,利用勾股定理进行求解即可.
(1)如图,作OE⊥AC于E,连接OM,ON,
∵⊙O与AB相切于点M,与CD相切于点N,
∴OM⊥AB,ON⊥CD,
∵OA平分∠BAC,OE⊥AC,
∴OM=OE,
∴AC是⊙O的切线,
∵ON=OE,ON⊥CD,OE⊥AC,
∴OC平分∠ACD,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠AOC=180°﹣![]() (∠DAC+∠ACD)=180°﹣45°=135°.
(∠DAC+∠ACD)=180°﹣45°=135°.
(2)∵AD,CD,AC是⊙O的切线,M,N,E是切点,
∴AM=AE,DM=DN,CN=CE=3,设DM=DN=x,AM=AE=y,
∵AB=AC,
∴BD=3﹣x,
在Rt△BDC中,∵BC2=BD2+CD2,
∴20=(3﹣x)2+(3+x)2,
∵x>0,
∴x=1,
∴DM=1.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目