Question

如图①，在△ABC中，CD、CE分别是△ABC的高和角平分线，∠BAC=α，∠B=β（α＞β）．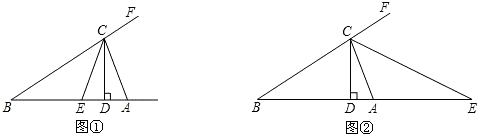
（1）若α=70°，β=40°，求∠DCE的度数；
（2）试用α、β的代数式表示∠DCE的度数（直接写出结果）；
（3）如图②，若CE是△ABC外角∠ACF的平分线，交BA延长线于点E，且α-β=30°，求∠DCE的度数．

Answer 1

分析：（1）三角形的内角和是180°，已知∠BAC与∠ABC的度数，则可求出∠BAC的度数，然后根据角平分线的性质求出∠BCE，再利用三角形的一个外角等于和它不相邻的两个内角的和求出∠DEC的度数，进而求出∠DCE的度数；
（2）∠DCE=

α-β

2

．
（3）作∠ACB的内角平分线CE′，根据角平分线的性质求出∠ECE′=∠ACE+∠ACE′=

1

2

∠ACB+

1

2

∠ACF=90°，进而求出∠DCE的度数．

解答：解：（1）因为∠ACB=180°-（∠BAC+∠B）=180°-（70°+40°）=70°，
又因为CE是∠ACB的平分线，
所以∠ACE=

1

2

∠ACB=35°．
因为CD是高线，
所以∠ADC=90°，
所以∠ACD=90°-∠BAC=20°，
所以∠DCE=∠ACE-∠ACD=35°-20°=15°．

（2）∠DCE=

α-β

2

．

（3）如图，作∠ACB的内角平分线CE′，
则∠DCE′=

α-β

2

=15°．
因为CE是∠ACB的外角平分线，
所以∠ECE′=∠ACE+∠ACE′=

1

2

∠ACB+

1

2

∠ACF=

1

2

(∠ACB+∠ACF)=90°，
所以∠DCE=90°-∠DCE′=90°-15°=75°．
即∠DCE的度数为75°．

点评：本题考查三角形外角的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．解决（3），作辅助线是关键．