题目内容
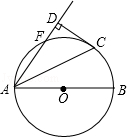
【题目】如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点, ![]() =
= ![]() =
= ![]() ,则CM+DM的最小值为 .
,则CM+DM的最小值为 . 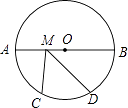
【答案】16
【解析】解:如图,作点C关于AB的对称点C′,连接C′D与AB相交于点M,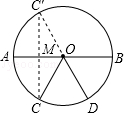
此时,点M为CM+DM的最小值时的位置,
由垂径定理, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() ,AB为直径,
,AB为直径,
∴C′D为直径,
∴CM+DM的最小值是16.
故答案是:16.
【考点精析】掌握圆心角、弧、弦的关系和轴对称-最短路线问题是解答本题的根本,需要知道在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目