题目内容
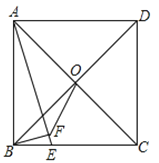
【题目】如图,已知正方形ABCD的边长为![]() ,对角线AC、BD交于点O,点E在BC上,且CE=2BE,过B点作BF⊥AE于点F,连接OF,则线段OF的长度为_________.
,对角线AC、BD交于点O,点E在BC上,且CE=2BE,过B点作BF⊥AE于点F,连接OF,则线段OF的长度为_________.
【答案】![]()
【解析】
先判断出∠OBF=∠CAE,从而得出△AOG≌△BOF,即可判断出△OFG是等腰直角三角形,再根据勾股定理和射影定理求出BF,AF,AG,即可得出FG.
如图,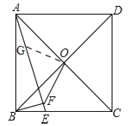
作OG⊥OF交AE于G,
∴OA=OB,∠FOG=90°,
∵AC,BD是正方形的对角线,
∴∠AOB=90°,
∴∠AOG=∠BOF,
∵BF⊥AE,
∴∠BAE+∠ABF=90°,
∵∠BAE=∠BAC∠CAE
∴∠OBF=∠ABF∠ABD=90°∠BAE∠ABD=90°∠BAC+∠CAE∠ABD=∠CAE,
在△AOG和△BOF中,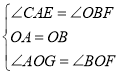
∴△AOG≌△BOF(ASA),
∴OG=OF,
∴△OFG是等腰直角三角形,
∵CE=2BE,BC=![]() ,
,
∴BE=![]() ,
,
根据勾股定理得,AE=![]() ,
,
在Rt△ABE中,
根据射影定理得,BF=1,AF=3,
∴AG=BF=1,
GF=AFBF=2,
∴OF=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目