题目内容
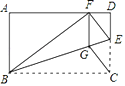
【题目】如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点
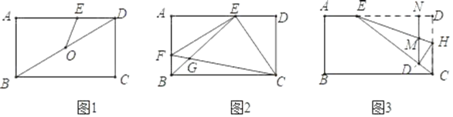
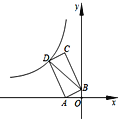
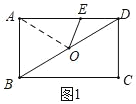
(1)如图 1,连接 BD,O 是对角线 BD 的中点,连接 OE.当 OE=DE 时,求 AE 的长;
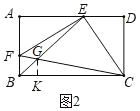
(2)如图 2,连接 BE,EC,过点 E 作 EF⊥EC 交 AB 于点 F,连接 CF,与 BE 交于点 G.当BE 平分∠ABC 时,求 BG 的长;
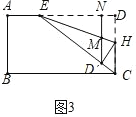
(3)如图 3,连接 EC,点 H 在 CD 上,将矩形 ABCD 沿直线 EH 折叠,折叠后点 D 落在 EC上的点 D′处,过点 D′作 D′N⊥AD 于点 N,与 EH 交于点 M,且 AE=1.![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先求出![]() ,进而求出
,进而求出![]() ,再判断
,再判断![]() ,即可得出结论;
,即可得出结论;
(2)先判断出![]() ,进而求出
,进而求出![]() ,再判断出
,再判断出![]() ,进而求得
,进而求得![]() ,最后利用勾股定理即可得出结论;
,最后利用勾股定理即可得出结论;
(3)先求出![]() ,再求出
,再求出![]() ,根据勾股定理求出
,根据勾股定理求出![]() ,
,![]() ,再判断出
,再判断出![]() ,
,![]() ,列出比例式,并根据同高三角形面积的比等于对应底边的比,即可得出结论;
,列出比例式,并根据同高三角形面积的比等于对应底边的比,即可得出结论;
解:(1)如图 1,连接![]() ,
,
在矩形![]() 中,
中,![]() ,
,
![]() 在
在![]() 中,根据勾股定理得
中,根据勾股定理得![]()
∵![]() 是
是![]() 的中点,
的中点,
![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
(2)∵![]() 平分
平分![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
如图 2,过点![]() 作
作![]() 于
于![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
设![]() ,则
,则![]()
![]()
解得:![]()
∴![]() ,
,
![]() 在
在![]() 中,
中,![]()
(3)如图 3,在矩形![]() 中,
中,![]() ,
,
∵![]()
∴![]() ,
,
∵![]() ,
,
∴在![]() 中,由勾股定理可得:
中,由勾股定理可得:![]() ,
,
由折叠知,![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]()
![]() 在
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]()
解得:![]()
∴![]()
∵![]()
∴![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
∵![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目