题目内容
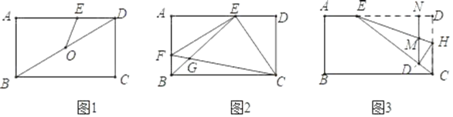
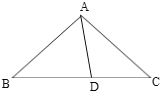
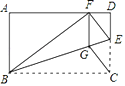
【题目】如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=6,AD=10,求四边形CEFG的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意和翻折的性质,可以得到△BCE≌△BFE,再根据全等三角形的性质和菱形的判定方法即可证明结论成立;
(2)根据题意和勾股定理,可以求得AF的长,进而求得EF和DF的值,从而可以得到四边形CEFG的面积.
(1)证明:由题意可得,△BCE≌△BFE,
∴∠BEC=∠BEF,FE=CE,
∵FG∥CE,
∴∠FGE=∠CEB,
∴∠FGE=∠FEG,
∴FG=FE,
∴FG=EC,
∴四边形CEFG是平行四边形,
又∵CE=FE,
∴四边形CEFG是菱形;
(2)∵矩形ABCD中,AB=6,AD=10,BC=BF,
∴∠BAF=90°,AD=BC=BF=10,
∴AF=8,
∴DF=2,
设EF=x,则CE=x,DE=6﹣x,
∵∠FDE=90°,
∴22+(6﹣x)2=x2,
解得,x=![]() ,
,
∴CE=![]() ,
,
∴四边形CEFG的面积是:CEDF=![]() ×2=
×2=![]() .
.

【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?