题目内容

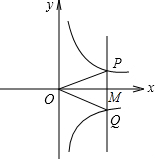如图，若点M是x轴正半轴上的任意一点，过点M作PQ∥y轴，分别交函数y1=
k1
x
（x＞0）和y2=
k2
x
（x＞0）的图象于点P和Q，连接OP、OQ，则下列结论正确的是（　　）
A、△POQ的面积是
1
2
（|K1|+|K2|）
B、
PM
QM
=
k1
k2
C、这两个函数的图象一定关于x轴对称
D、∠POQ不可能等于90°
练习册系列答案
相关题目
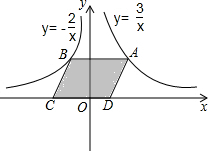如图，点A是反比例函数y=
3
x
（x＞0）的图象上任意一点，AB∥x轴交反比例函数y=-
2
x
的图象于点B，以AB为边作平行四边形ABCD，其中C、D在x轴上，则S平行四边形ABCD为（　　）
A、2B、3C、4D、5
函数y=-x与y=
k
x
（k≠0）的图象无交点，且y=
k
x
的图象过点A（1，y1），B（2，y2），则（　　）
A、y1＜y2
B、y1=y2
C、y1＞y2
D、y1，y2的大小无法确定
已知函数y=
k
x
和函数y=
1
2
x+1的图象交于A、B两点，点A的坐标为（2，2），以下结论：
①反比例函数的图象一定过点（-1，-4）；
②当x＞2时，
1
2
x+1＞
k
x
；
③点B的坐标是（-4，-1）；
④S△OCD=1．
其中正确的结论的个数是（　　）
A、1B、2C、3D、4
如图，△ABC的边BC=y，BC边上的高AD=x，△ABC的面积为3，则y与x的函数图象大致是（　　）
A、B、C、D、
在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是（　　）
A、120°B、90°C、60°D、30°
如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D．则BD的长为（　　）
A、
2
3
5
B、
3
4
5
C、
4
5
5
D、
3
5
5
如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”，它解决的数学问题是（　　）
A、黄金分割B、垂径定理C、勾股定理D、正弦定理
如图，△ABC的中线BD、CE交于点O，连接OA，点G、F分别为OC、OB的中点，BC=4，AO=3，则四边形DEFG的周长为（　　）
A、6B、7C、8D、12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网