题目内容
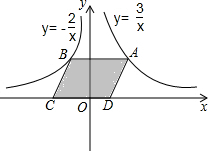 如图,点A是反比例函数y=
如图,点A是反比例函数y=| 3 |
| x |
| 2 |
| x |
| A、2 | B、3 | C、4 | D、5 |
练习册系列答案
相关题目
若函数y=
的图象分别位于第二、四象限,则m的取值范围是( )
| m+1 |
| x |
| A、m>0 | B、m<0 |
| C、m>-1 | D、m<-1 |
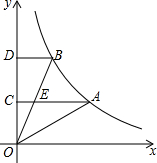 如图,A、B是反比例函数y=
如图,A、B是反比例函数y=| 2 |
| x |
| A、S1=S2 |
| B、S1<S2 |
| C、S1>S2 |
| D、无法确定 |
已知两点P1(x1,y1)、P2(x2,y2)在函数y=
的图象上,当x1>x2>0时,下列结论正确的是( )
| 5 |
| x |
| A、0<y1<y2 |
| B、0<y2<y1 |
| C、y1<y2<0 |
| D、y2<y1<0 |
下列各点中,在函数y=-
的图象上的点是( )
| 12 |
| x |
| A、(3,4) |
| B、(-2,-6) |
| C、(-2,6) |
| D、(-3,-4) |
反比例函数y=-
图象上的两个点为(x1,y1)、(x2,y2),且x1>0>x2,则下列式子一定成立的是( )
| 9 |
| x |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、y1≥y2 |
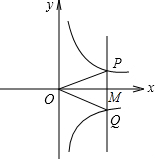 如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y1=
如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y1=| k1 |
| x |
| k2 |
| x |
A、△POQ的面积是
| ||||
B、
| ||||
| C、这两个函数的图象一定关于x轴对称 | ||||
| D、∠POQ不可能等于90° |





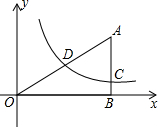 如图,已知双曲线y=
如图,已知双曲线y=