题目内容
如图，△ABC的边BC=y，BC边上的高AD=x，△ABC的面积为3，则y与x的函数图象大致是（ ）A、 | B、 | C、 | D、 |
练习册系列答案
相关题目
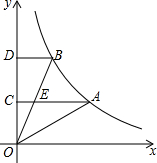如图，A、B是反比例函数y=| 2 |
| x |
| A、S1=S2 |
| B、S1＜S2 |
| C、S1＞S2 |
| D、无法确定 |
已知反比例函数y=
（x＞0）的图象经过点（m，y1）、（m+1，y2）、（m+2，y3），则下列关于y1+y3与y2的大小关系正确的是（ ）
| 3 |
| x |
| A、y1+y3＞2y2 |
| B、y1+y3＜2y2 |
| C、y1+y3=2y2 |
| D、不能确定 |
如图，直线y=-x+a-1与双曲线y=| -2 |
| x |
| A、0 | B、1 | C、2 | D、3 |
如图，在平面直角坐标系中，矩形OABC的边OA、OC分别与x、y轴重合，其中心为点D，函数y=| k |
| x |
| CF |
| BF |
| AE |
| BE |
A、
| ||||
B、
| ||||
C、
| ||||
| D、与k的值有关 |
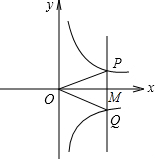如图，若点M是x轴正半轴上的任意一点，过点M作PQ∥y轴，分别交函数y1=| k1 |
| x |
| k2 |
| x |
A、△POQ的面积是
| ||||
B、
| ||||
| C、这两个函数的图象一定关于x轴对称 | ||||
| D、∠POQ不可能等于90° |
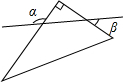如图，已知∠α=130°，则∠β=（ ）| A、30° | B、40° | C、50° | D、65° |
如图，Rt△ABC中，∠A=90°，∠ABC=60°，AC=3．点P是边BC上一点，点Q是边AC上一点（不与点A、C重合），且BP=PQ，则BP的取值范围是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图，等边△ABC中，点D、E分别为边AB、AC的中点，则∠DEC的度数为（ ）| A、30° | B、60° | C、120° | D、150° |