题目内容
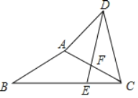
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AC上一点,连接BD.过点C作CE⊥BD于点E.点F是AB垂直平分线上一点,连接BF、EF.
(1)若AD=4![]() ,tan∠BCE=
,tan∠BCE=![]() ,求AB的长;
,求AB的长;
(2)当点F在AC边上时,求证:∠FEC=45°.

【答案】(1) AB=18;(2)证明见解析;
【解析】
(1)先过点D作DM⊥AB于点M,构造等腰直角三角形,求得DM=AM=4,再根据∠ABD=∠BCE,得出tan∠BCE=tan∠ABD,求得BM=14,进而根据AB=AM+BM进行计算;
(2)在CE上截取CN=BE,连接FN,先判定△BEF≌△CFN,得出△EFN是等腰直角三角形,根据等腰三角形的性质即可得到结论.
(1)如图,过点D作DM⊥AB于点M.
∵∠ABC=90°,AB=BC,∴∠A=45°,∴AM=DM.
∵AD=4![]() ,∴DM=AM
,∴DM=AM![]() AD=4.
AD=4.
∵CE⊥BD,∴∠BEC=90°=∠ABC,∴∠BCE+∠EBC=90,∠EBC+∠ABD=90°,∴∠ABD=∠BCE,∴tan∠BCE=tan∠ABD![]() ,即
,即![]() ,∴BM=14,∴AB=AM+BM=4+14=18;
,∴BM=14,∴AB=AM+BM=4+14=18;
(2)∵F是AB的垂直平分线上的点,∴AF=BF,∴∠A=∠ABF=45°.
∵∠ABC=90°,∴∠FBC=45°,∴∠FBC=∠FCB,且∠ABD=∠BCE,∴BF=CF,∠EBF=∠ECF,如图,在CE上截取CN=BE,连接FN.
∵BF═CF,∠EBF=∠ECF,∴△BEF≌△CFN,(SAS),∴FN=EF,∠BFE=∠CFN.
∵∠FCB=∠FBC=45°,∴∠BFC=90°,∴∠CFN+∠BFN=90°,∴∠BFE+∠BFN=90°,∴∠EFN=90°,且EF=FN,∴△EFN是等腰直角三角形,∴∠FEC=45°.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案