题目内容
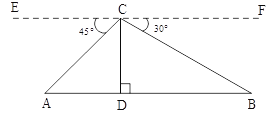
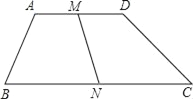
【题目】在梯形ABCD中,AD∥BC,∠B+∠C=90°,AB=5,CD=12,M,N分别为AD,BC的中点,则线段MN=_____.
【答案】6.5
【解析】
过点M作ME∥AB,MF∥CD,由此得到∠MEN=∠B,∠NFM=∠C,又∠B+∠C=90°,可以推出∠EMF=90°,然后根据平行四边形的性质可以得到ME=AB=5,MF=CD=12,AM=DM,BN=CN,再利用斜边上的中线等于斜边的一半即可证明MN=![]() EF,最后就可以求出MN.
EF,最后就可以求出MN.
解:如图:
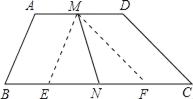
过点M作ME∥AB,MF∥CD,
∴∠MEN=∠B,∠NFM=∠C,
∵∠B+∠C=90°,
∴∠MEF+∠MFE=90°,
∴∠EMF=90°.
∵AD∥BC,
∴ME=AB=5,MF=CD=12,AM=DM,BN=CN.
∴EF=13,EN=FN.
∴MN=![]() EF=6.5.
EF=6.5.
故答案为:6.5

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目