题目内容
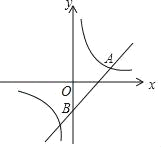
【题目】如图,在⊙O中,半径OC=6,D为半径OC上异于O,C的点,过点D作AB⊥OC,交⊙O于A,B,点E在线段AB上,AE=CE,点P在线段EC的延长线上,PB=PE.
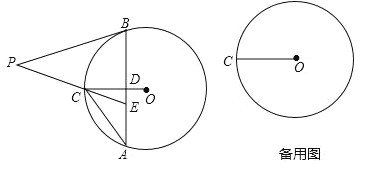
(1)若OD=2,求弦AB的长;
(2)当点D在线段OC(不含端点)上移动时,直线PB与⊙O有怎样的位置关系?请说明理由;
(3)点Q是⊙O上的一个动点,若点D为OC中点时,线段PQ的最小值为多少?请说明理由.
【答案】(1)![]() ;(2)PB与⊙O相切;(3)
;(2)PB与⊙O相切;(3)![]() .
.
【解析】
(1)连接OB,由OB=OC=6,OD=2,利用勾股定理可得BD的长,根据垂径定理可得答案;
(2)连接OB,OA,OE,先证△AOE≌△COE得∠OAE=∠OCE,结合∠OBA=∠OAB知∠OCE=∠OBA,根据PB=PE知∠PBE=∠PEB,根据∠OCE+∠PEB=90°得∠OBA+∠PBE=90°,由切线的判定可得答案;
(3)先确定线段PQ的最小值时Q的位置:因为OQ为半径,是定值4,则PQ+OQ的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,先求AE的长,从而得PB的长,最后利用勾股定理求OP的长,与半径的差就是PQ的最小值.
(1)如图1,连接OB,
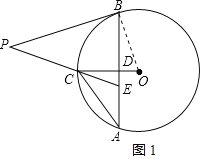
∵OB=OC=6,OD=2,
∴BD=![]() ,
,
则AB=2BD=8![]() ;
;
(2)如图2,连接OB,OA,OE,
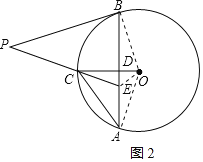
∵OB=OA=OC,
∴∠OBA=∠OAB,
又∵OE=OE,AE=CE,
∴△AOE≌△COE(SSS),
∴∠OAE=∠OCE,
∴∠OCE=∠OBA,
∵PB=PE,
∴∠PBE=∠PEB,
∵AB⊥CD,
∴∠OCE+∠PEB=90°,
∴∠OBA+∠PBE=90°,即∠PBO=90°,
∴OB⊥PB,
又OB是⊙O的半径,
∴PB与⊙O相切;
(3)线段PQ的最小值为2![]() -6,理由如下:
-6,理由如下:
∵D为OC的中点,
∴OD=![]() OC=
OC=![]() OB,
OB,
在Rt△OBD中,∠OBD=30°,
∴∠BOC=60°,
∵OB=OC,
∴△BOC是等边三角形,
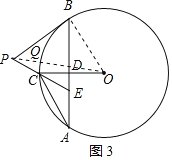
∵Q为⊙O任意一点,
连接PQ、OQ,
因为OQ为半径,是定值4,
则PQ+OQ的值最小时,PQ最小,
当P、Q、O三点共线时,PQ最小,
∴Q为OP与⊙O的交点时,PQ最小,
∠A=![]() ∠COB=30°,
∠COB=30°,
∴∠PEB=2∠A=60°,
∠ABP=90°-30°=60°,
∴△PBE是等边三角形,
Rt△OBD中,BD=![]() =3
=3![]()
∴AB=2BD=6![]() ,
,
设AE=x,则CE=x,ED=3![]() -x,
-x,
Rt△CDE中,x2=32+(3![]() -x)2,
-x)2,
解得:x=2![]() ,
,
∴BE=PB=6![]() -2
-2![]() =4
=4![]() ,
,
Rt△OPB中,OP=![]() ,
,
∴PQ=2![]() -6,
-6,
则线段PQ的最小值是2![]() -6.
-6.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量 | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,设购进
种商品数量的4倍,设购进![]() 种商品
种商品![]() 件,获得的利润为
件,获得的利润为![]() 元,
元,
①请列出![]() 与
与![]() 的函数关系式
的函数关系式
②求出获利最大的进货方案,并确定最大利润.