题目内容
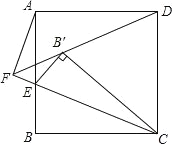
【题目】如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为_____.
【答案】![]()
【解析】
作CH⊥B′D于H,连接AC,根据翻转变换的性质、等腰直角三角形的性质和相似三角形的性质得到△AFC∽△HCD,证明△AFE∽△CBE,根据相似三角形的对应边成比例即可得出结论.
作CH⊥B′D于H,连接AC,由翻折变换的性质得:∠BCE=∠B′CE,CB′=CD,CH⊥B′D,∴∠B′CH=∠DCH,∴∠ECH=45°.
∵∠ACF+∠BCE=45°,∴∠ACF=∠DCH,∴![]()
![]() ,∴
,∴![]() .
.
又∵∠ACF=∠DCH,∴△AFC∽△HCD,∴∠AFC=∠DHC=90°,∴∠AFC=∠CBE,又∠AEF=∠CEB,∴△AFE∽△CBE,∴![]() ,即
,即![]() ,解得:AF
,解得:AF![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目