题目内容
【题目】已知:在△ABC中,AB=AC=6,∠B=30°,E为BC上一点,BE=2EC,DE=DC,∠ADC=60°,则AD的长_____.
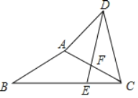
【答案】2![]()
【解析】
过A点做AG⊥BC,连接AE,可得△BAE为RT△,且∠AEB=60![]() ,∠AEC=120
,∠AEC=120![]() ,AE=CE,四边形DAEC共圆,可得∠ADE=∠CDE=
,AE=CE,四边形DAEC共圆,可得∠ADE=∠CDE=![]() ∠ADC=60°=30
∠ADC=60°=30![]() ,过点A做AO⊥CD与O点,可得△OAC为等腰直角三角形,可得OA的长,进而求出AD的长.
,过点A做AO⊥CD与O点,可得△OAC为等腰直角三角形,可得OA的长,进而求出AD的长.
解:如图: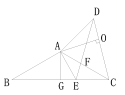
过A点做AG⊥BC,连接AE,![]() AB=AC
AB=AC
![]() G为BC的中点,在RT△ABG中,AB=AC=6,∠B=30°
G为BC的中点,在RT△ABG中,AB=AC=6,∠B=30°
![]() ∠ACB=30°,AG=
∠ACB=30°,AG=![]() =3,BG=CG=
=3,BG=CG=![]() ,
,
![]() BC=2BG=
BC=2BG=![]() ,
,
![]() 又BE=2EC,可得BE=
又BE=2EC,可得BE=![]() ,CE=
,CE=![]() ,
,![]() GE=
GE=![]()
在RT△AGE中,AE=![]() =
=![]() =
=![]() ,
,
![]() AE=CE=
AE=CE=![]() ,
,
在△BAE中,AB=6,BE=![]() ,AE=
,AE=![]() ,
,
可得![]()
![]() △BAE为RT△,∠BAE=90
△BAE为RT△,∠BAE=90![]() ,
,
![]() ∠B=30
∠B=30![]() ,
,
![]() ∠AEB=60
∠AEB=60![]() , ∠AEC=120
, ∠AEC=120![]() ,
,
在四边形DAEC中,∠ADC=60°,∠AEC=120![]() ,
,
![]() ∠ADC+∠AEC=180°,
∠ADC+∠AEC=180°,
![]() 四边形DAEC共圆,
四边形DAEC共圆,
![]() AE=CE=
AE=CE=![]()
![]() ∠ADE=∠CDE=
∠ADE=∠CDE=![]() ∠ADC=60°=30
∠ADC=60°=30![]() ,
,
过点A做AO⊥CD与O点,
在△DCE中,∠CDE=30![]() ,DE=DC
,DE=DC
![]() ∠DCE=
∠DCE=![]() =75
=75![]() ,
,![]() ∠ACB=30
∠ACB=30![]()
![]() ∠OCA=45
∠OCA=45![]() ,△OAC为等腰直角三角形
,△OAC为等腰直角三角形
在RT△OAC中,AC=6,∠OCA=45![]() ,
,![]() AO= AC
AO= AC![]() =
=![]() ,
,
在RT△AOD中, AO=![]() ,∠ADO=60
,∠ADO=60![]() ,可得AD=
,可得AD=![]() =
=![]() .
.
故答案:![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目