题目内容
【题目】知识背景：我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在第十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边，进而解决问题.
问题：如图1，
是等腰三角形，
，
是
的中点，以
为腰作等腰
，且满足
，连接
并延长交
的延长线于点
，试探究与
之间的数量关系.
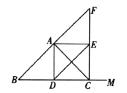
图1
发现：（1）与之间的数量关系为 .
探究：（2）如图2，当点是线段上任意一点（除
、
外）时，其他条件不变，试猜想与之间的数量关系，并证明你的结论.
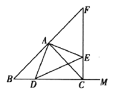
图2
拓展：（3）当点在线段的延长线上时，在备用图中补全图形，并直接写出
的形状.
备用图
【答案】（1）
；（2），证明见解析；（3）画图见解析，等腰直角三角形.
【解析】
（1）根据等腰三角形的性质即可得；
（2）由等腰直角三角形的性质可得
，再根据全等三角形的性质及等角对等边即可证明；
（3）作出图形，根据等腰三角形性质易证，进而根据角度的代换，得出结论．
解：（1）.
∵△ABC是等腰三角形，且
，
，
.
，
，
，
.
是以
为腰的等腰三角形，
.
在
与
中，
，
，
，
，
.
，
，
，
，
，
.
（2）.
证明：
是等腰三角形，且，
，.
，
，
，
.
是以为腰的等腰三角形，
.
在与中，，，，
，
.
，
，
，
，
，
.
（3）
是等腰直角三角形.
提示：如图，
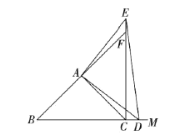
是等腰三角形，，
，.
，
，
，
.
是以为腰的等腰三角形，
.
在与中，，，，
，
.
，
，
，
，
，
是等腰三角形，
，
是等腰直角三角形.
练习册系列答案
科学实验活动册系列答案
相关题目
