Question

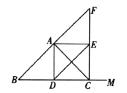
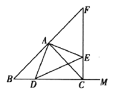
【题目】如图，已知点在上，延长直径到点，连接，．

求证：是的切线；

若，且，是下半圆弧的中点，求的长．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

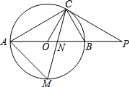
（1）由于OA=OC，那么∠OAC=∠OCA，则∠COB=2∠OCA，又∠COB=2∠PCB，可求∠OCA=∠PCB，而AB是直径，可知∠OCA+∠OCB=90°，从而有∠PCB+∠OCB=90°，即∠OCP=90°，从而可证CP是⊙O切线；
（2）连接BM，由于M是弧AB中点，那么AM=BM，而∠AMB=90°，易知∠MAB=∠MBA=45°，而AC=CP，则∠P=∠CAO，又∠BCP=∠CAO，从而有∠P=∠BCP，即BC=BP=3，而∠CBO=2∠P，∠BOC=2∠CAO，于是∠BOC=∠CBO，而OB=OC，那么可证△BOC是等边三角形，从而有OB=BC=3，即AB=6，在Rt△AMB中，利用特殊三角函数值可求AM．

∵，

∴，

∴，

∵，

∴，

∵是直径，

∴，

∴，

∴，

∴，

∵点在上，

∴是的切线；

连接．

∵是下半圆弧中点，

∴弧弧，

∴，

∵是直径，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

∵，

∴，

∴是等边三角形，

∴，

∵，

∴，

∴，

在中，，．