题目内容
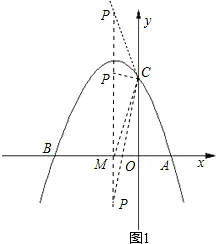
如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.

(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.

(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(1)由题知:
|
解得:
|
∴所求抛物线解析式为:
y=-x2-2x+3;
(2)∵抛物线解析式为:
y=-x2-2x+3,
∴其对称轴为x=
| -2 |
| 2 |
∴设P点坐标为(-1,a),当x=0时,y=3,
∴C(0,3),M(-1,0)
∴当CP=PM时,(-1)2+(3-a)2=a2,解得a=
| 5 |
| 3 |
∴P点坐标为:P1(-1,
| 5 |
| 3 |
∴当CM=PM时,(-1)2+32=a2,解得a=±
| 10 |
∴P点坐标为:P2(-1,
| 10 |
| 10 |
∴当CM=CP时,由勾股定理得:(-1)2+32=(-1)2+(3-a)2,解得a=6,
∴P点坐标为:P4(-1,6)
综上所述存在符合条件的点P,其坐标为P(-1,
| 10 |
| 10 |

或P(-1,6)或P(-1,
| 5 |
| 3 |
(3)过点E作EF⊥x轴于点F,设E(a,-a2-2a+3)(-3<a<0)
∴EF=-a2-2a+3,BF=a+3,OF=-a
∴S四边形BOCE=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 63 |
| 8 |
∴当a=-
| 3 |
| 2 |
| 63 |
| 8 |
此时,点E坐标为(-
| 3 |
| 2 |
| 15 |
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 1cm的速度作匀速运动,最后点E与点B重合.
1cm的速度作匀速运动,最后点E与点B重合.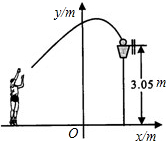 单位:m).请你根据所得的解析式,回答下列问题:
单位:m).请你根据所得的解析式,回答下列问题: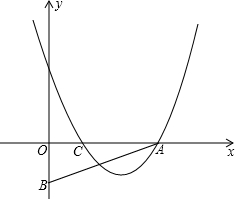 C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
