题目内容
某玩具厂授权生产工艺品福娃,每日最高产量为30只,且每日生产的产品全部出售.已知生产x只福娃的成本为R(元),每只售价P(元),且R,P与x的表达式分别为R=50+3x,P=170-2x.当日产量为多少时,可获得最大利润?最大利润是多少?
假设生产x只福娃,可获得利润y元,
y=px-R,
=(170-2x)x-(50+3x),
=-2x2+167x-50,
当x=-
时,y最大=
,
x=-
=-
=
>30,根据二次函数增减性x<
时,y随x的增大而增大,
又因为每日最高产量为30只,
所以当x=30只时,y取最大值为:-2×302+167×30-50=3160元.
答:日产量为30只时,可获得最大利润,最大利润是3160元.
y=px-R,
=(170-2x)x-(50+3x),
=-2x2+167x-50,
当x=-
| b |
| 2a |
| 4ac-b2 |
| 4a |
x=-
| b |
| 2a |
| 167 |
| 2×(-2) |
| 167 |
| 4 |
| 167 |
| 4 |
又因为每日最高产量为30只,
所以当x=30只时,y取最大值为:-2×302+167×30-50=3160元.
答:日产量为30只时,可获得最大利润,最大利润是3160元.

练习册系列答案
相关题目

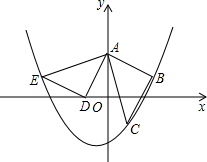 B(2,1),C(1,-1),将三角板绕A点顺时针转α°后,使B点与x轴上的点D(-1,0)重合.
B(2,1),C(1,-1),将三角板绕A点顺时针转α°后,使B点与x轴上的点D(-1,0)重合.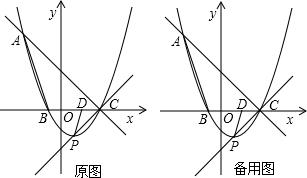
 C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
 金150万元,请问能否将这30户移民农户全部安置?并说明理由.
金150万元,请问能否将这30户移民农户全部安置?并说明理由.
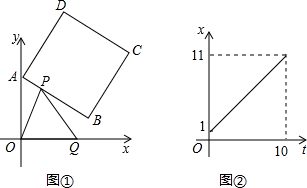 能,写出所有符合条件的t的值;若不能,请说明理由.
能,写出所有符合条件的t的值;若不能,请说明理由.