题目内容
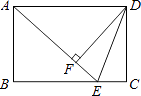
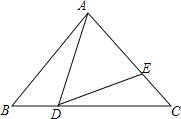
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC=2,BC=![]() .点D从B点开始运动到C点结束(点D和B、C均不重合),DE交AC于E,∠ADE=45°,当△ADE是等腰三角形时,AE的长度为__________.
.点D从B点开始运动到C点结束(点D和B、C均不重合),DE交AC于E,∠ADE=45°,当△ADE是等腰三角形时,AE的长度为__________.
【答案】1或4-2![]()
【解析】
分类讨论:当EA=ED,△ADE为等腰三角形,由∠ADE=45°得到∠EAD=45°,∠AED=90°,则AD平分∠BAC,AD⊥BC,DE⊥AC,然后根据等腰直角三角形的性质得到DE=![]() AC=1;当DA=DE,△ADE为等腰三角形,由∠ADE=45°得到∠ADB+∠EDC=180°-45°=135°,而∠EDC+∠DEC=135°,所以∠ADB=∠DEC,根据三角形相似的判定得到△ABD∽△DCE,则BD:CE=AB:DC=AD:DE,利用AD=DE得到AB=DC=2,BD=CE;由于∠BAC=90°,AB=AC=2,根据等腰直角三角形的性质得BC=2
AC=1;当DA=DE,△ADE为等腰三角形,由∠ADE=45°得到∠ADB+∠EDC=180°-45°=135°,而∠EDC+∠DEC=135°,所以∠ADB=∠DEC,根据三角形相似的判定得到△ABD∽△DCE,则BD:CE=AB:DC=AD:DE,利用AD=DE得到AB=DC=2,BD=CE;由于∠BAC=90°,AB=AC=2,根据等腰直角三角形的性质得BC=2![]() ,所以BD=2
,所以BD=2![]() -2=EC,然后根据AE=AC-EC进行计算.
-2=EC,然后根据AE=AC-EC进行计算.
解:当EA=ED,△ADE为等腰三角形,
∵∠ADE=45°,
∴∠EAD=45°,∠AED=90°,
∵∠BAC=90°,
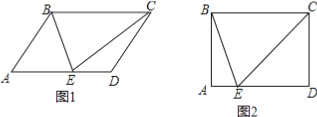
∴AD平分∠BAC,AD⊥BC,DE⊥AC,如图1,
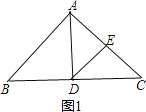
∵AB=AC=2,
∴DE=![]() AC=1;
AC=1;
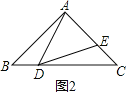
当DA=DE,△ADE为等腰三角形,如图2
∵∠ADE=45°,
∴∠ADB+∠EDC=180°-45°=135°,
而∠EDC+∠DEC=135°,
∴∠ADB=∠DEC,
而∠B=∠C,
∴△ABD∽△DCE,
∴BD:CE=AB:DC=AD:DE,
而AD=DE,
∴AB=DC=2,BD=CE,
∵BC=2![]() ,
,
∴BD=2![]() -2=EC,
-2=EC,
∴AE=AC-EC=2-(2![]() -2)=4-2
-2)=4-2![]() .
.
故答案为1或4-2![]() .
.

练习册系列答案
相关题目