题目内容
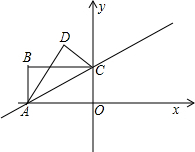
如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B的坐标分别A(-2
,0)、B(-2
,2),∠CAO=30°.
(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
| 3 |
| 3 |
(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.

(1)由题意得,OA=2
,∠CAO=30°,
则OC=OAtan∠CAO=2,
即点C的坐标为(0,2),
设直线AC的解析式为:y=kx+b,将点A及点C的坐标代入得:
,
解得:
,
故直线AC的函数表达式为:y=
x+2.
(2)过点D作DE⊥OA于点E,
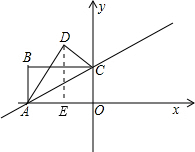
∵∠CAO=30°,
∴∠DAE=60°,
又∵AD=AO=2
,
∴DE=3,AE=
,
∴OE=
,
故点D的坐标为(-
,3).
(3)
①当AD为平行四边形的一边时,点P的位置有两个,分别为P1、P2,
当点P位于P1位置时,DP1=AO,
此时可得点P的坐标为(
,3);
当点P位于P2位置时,
∵OD=AD,△AOD是等边三角形,
∴点P2与点D关于x轴对称,
此时可得点P的坐标为(-
,-3);
②当AD为平行四年行的对角线时,点P的位置有一个,在P3的位置,
此时DP3=AO,
故可得点P的坐标为(-3
,3).
综上可得存在点P的坐标,使得以A、O、D、P为顶点的四边形为平行四边形,点P的坐标为(
,3)或(-
,-3)或(-3
,3).
| 3 |
则OC=OAtan∠CAO=2,
即点C的坐标为(0,2),
设直线AC的解析式为:y=kx+b,将点A及点C的坐标代入得:
|
解得:
|
故直线AC的函数表达式为:y=
| ||
| 3 |
(2)过点D作DE⊥OA于点E,

∵∠CAO=30°,
∴∠DAE=60°,
又∵AD=AO=2
| 3 |
∴DE=3,AE=
| 3 |
∴OE=
| 3 |
故点D的坐标为(-
| 3 |
(3)

①当AD为平行四边形的一边时,点P的位置有两个,分别为P1、P2,
当点P位于P1位置时,DP1=AO,
此时可得点P的坐标为(
| 3 |
当点P位于P2位置时,
∵OD=AD,△AOD是等边三角形,
∴点P2与点D关于x轴对称,
此时可得点P的坐标为(-
| 3 |
②当AD为平行四年行的对角线时,点P的位置有一个,在P3的位置,
此时DP3=AO,
故可得点P的坐标为(-3
| 3 |
综上可得存在点P的坐标,使得以A、O、D、P为顶点的四边形为平行四边形,点P的坐标为(
| 3 |
| 3 |
| 3 |

练习册系列答案
相关题目
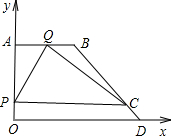 点Q也随之停止运动.
点Q也随之停止运动.




