题目内容
如图,直角坐标系中,有一半径为
的动圆⊙M,其圆心M从点(3,6)出发以每秒0.5个单位长度的速度沿y轴方向向下运动,当⊙M与直线y=x相切时,则⊙M运动的时间为______秒.

| 2 |

若圆M在上方与直线y=x相切,此时切点为B,如图1所示: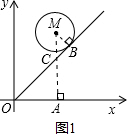
连接MB,则有MB⊥OB,过M作MA⊥x轴,与OB交于点C,
∵圆M的半径为
,即MB=
,∠MCB=∠OCA=∠COA=45°,
在Rt△MCB中,由MB=BC=
,
利用勾股定理得:MC=2,又M(3,6),
∴OA=AC=3,
则MA=MC+CA=2+3=5,
∴M运动了1个单位,又M的运动速度为每秒0.5个单位长度,
则此时用的时间为2秒;
若M在下方与直线y=x相切,此时切点为D,如图2所示:
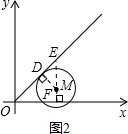 连接MD,过M作x轴的垂线,交y=x于E,交x轴于F,
连接MD,过M作x轴的垂线,交y=x于E,交x轴于F,
∵M(3,6),又∠EOF=∠DEF=45°,
∴OF=EF=3,DE=DM=
,
在Rt△DEM中,根据勾股定理得:EM=2,
此时MF=EF-EM=3-2=1,即M运动的路程为5个单位长度,
则此时用的时间是10秒,
综上,圆M的运动时间是2或10秒.
故答案为:2或10秒

连接MB,则有MB⊥OB,过M作MA⊥x轴,与OB交于点C,
∵圆M的半径为
| 2 |
| 2 |
在Rt△MCB中,由MB=BC=
| 2 |
利用勾股定理得:MC=2,又M(3,6),
∴OA=AC=3,
则MA=MC+CA=2+3=5,
∴M运动了1个单位,又M的运动速度为每秒0.5个单位长度,
则此时用的时间为2秒;
若M在下方与直线y=x相切,此时切点为D,如图2所示:
 连接MD,过M作x轴的垂线,交y=x于E,交x轴于F,
连接MD,过M作x轴的垂线,交y=x于E,交x轴于F,∵M(3,6),又∠EOF=∠DEF=45°,
∴OF=EF=3,DE=DM=
| 2 |
在Rt△DEM中,根据勾股定理得:EM=2,
此时MF=EF-EM=3-2=1,即M运动的路程为5个单位长度,
则此时用的时间是10秒,
综上,圆M的运动时间是2或10秒.
故答案为:2或10秒

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
 极性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的函数图象为折线OA-AB-BC,如图所示.
极性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的函数图象为折线OA-AB-BC,如图所示.
 我们就称直线l1与直线l2互相平行.解答下面的问题:
我们就称直线l1与直线l2互相平行.解答下面的问题:
