题目内容
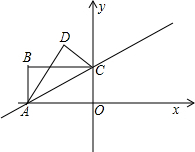
如图,直角坐标系中,正方形CDEF的边长为4,且CD∥y轴,直线y=-
x-1过点C,且交x轴,y轴于点A、B,若点P沿正方形ABCD运动一周,则以P为圆心、
为半径的圆动与直线CB相切的次数为( )

| 1 |
| 2 |
| 5 |
| A.一次 | B.两次 | C.三次 | D.四次 |

如图,作PH⊥BC于H,GM⊥BC与M,PN⊥CF,
∴∠PHS=∠GMC=∠PNC=90°.
∵四边形CDEF是正方形,
∴∠E=∠F=∠FCD=∠D=90°,CD=DE=EF=CF=4.CD∥y轴,
∴∠HPN=∠MGC=∠BAO,
∵直线y=-
x-1,当y=0时,x=-2,
当x=0时,y=-1,
∴A(-2,0),B(0,-1),
∴OA=2,OB=1,
∴tan∠OAB=
,
∴tan∠HPN=tan∠MGC=
.
当PH=
时,HS=
,
在Rt△PHS中,由勾股定理得:
PS=
,
∴SN=
,
∴NC=3,
∴PD=3,
∴P点运动到离D点的距离为3时,⊙P与直线相切,
当P点运动到G点,GM=
时,则MA=
,
在Rt△GMC中,由勾股定理,得
GC=
,
∴DG=
,
∴P点运动到离D点的距离为
时,⊙P与直线相切,
∴⊙P与直线CB相切2次.
故选B.
∴∠PHS=∠GMC=∠PNC=90°.
∵四边形CDEF是正方形,
∴∠E=∠F=∠FCD=∠D=90°,CD=DE=EF=CF=4.CD∥y轴,
∴∠HPN=∠MGC=∠BAO,
∵直线y=-
| 1 |
| 2 |
当x=0时,y=-1,
∴A(-2,0),B(0,-1),
∴OA=2,OB=1,
∴tan∠OAB=
| 1 |
| 2 |
∴tan∠HPN=tan∠MGC=
| 1 |
| 2 |
当PH=
| 5 |
| ||
| 2 |
在Rt△PHS中,由勾股定理得:
PS=
| 5 |
| 2 |
∴SN=
| 3 |
| 2 |
∴NC=3,
∴PD=3,

∴P点运动到离D点的距离为3时,⊙P与直线相切,
当P点运动到G点,GM=
| 5 |
| ||
| 2 |
在Rt△GMC中,由勾股定理,得
GC=
| 5 |
| 2 |
∴DG=
| 3 |
| 2 |
∴P点运动到离D点的距离为
| 3 |
| 2 |
∴⊙P与直线CB相切2次.
故选B.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目